corrigés - Jean

f∃a∈R,∃b∈R,∀x∈R, a ≤f(x)≤b∃M∈R,∀x∈
R,|f(x)| ≤ M
f∀a∈R,∀b∈R,∃x∈R, f(x)<
a f(x)> b ∀M∈R,∃x∈R,|f(x)|> M
f g ∃x∈R, f(x) = g(x)
∀x∈R, f(x)6=g(x)
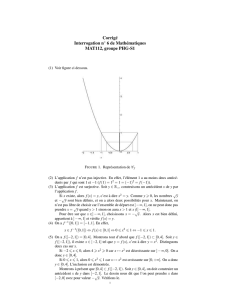
x7→ x2
∀M∈R,∃x∈R,|x2|> M
M∈Rx=p|M|+ 1 x2=|M|+1
x2> M x 7→ x2
x7→ cos2(x) + 2
∀x∈R,−1≤cos(x)≤1∀x∈R,|cos(x)| ≤ 1
x∈R0≤cos2(x)≤1 2 ≤cos2(x)+2≤3
x
a= 2 b= 3
x2= cos2(x)+2
g:x7→ x2−(cos2(x) + 2) R
g(0) = −3g(π) = π2−3>0g
]0, π[∃x∈]0, π[, g(x)=0 ∃x∈]0, π[, x2= cos2(x) + 2
∀n∈N,(6|n∧4|n) =⇒24|n
n= 12
n
∃n∈N,6|n4|n24 -n.
∀n∈N,(6|n∧n|40) =⇒n∈ P

∃n∈N,6|n n|40 n /∈ P.
∀p∈ P,∀a∈N,∀b∈N,(p|a p|b=⇒p|a+b
2)
p= 2 a= 4 b= 6 p∈ P p|a p|b p
a b
∀n∈N\ {0,1},∃p∈ P,∃q∈ P,2n=p+q
∀n∈N,2n−1∈ P =⇒n∈ P 2n−1
n
∀n∈N, n /∈ P =⇒2n−1/∈ P
n∈Nn n = 0
n= 1 n6= 0 n6= 1 n
r s n =rs r 6= 1 s6= 1
2n−1
2n−1=2rs −1 = (2r)s−1a= 2r
2n−1 = as−1s= (a−1)(as−1+as−2+···+a2+a+ 1) = (a−1) Ps−1
i=0 ai
r≥1a≥4a−1>1s6= 1
2n−1
2n−1n
∀x∈R, x2≥x
x= 1/2x2= 1/4
x
∀x∈R,∃!y∈R, xy = 1
R
∃x∈R,(∀y∈R, xy 6= 1) (∃y1∈R,∃y2∈R, y16=
y2xy1=xy2= 1)
∀x∈R∗,∃!y∈R, xy = 1
∀x∈R,∃a∈Z∗,∃b∈Z,∃c∈Z, ax2+bx +c= 0

π
π2π
π
π
3
√2
X3−2
x=3
√2∀a∈Z∗,∀b∈Z,∀c∈Z, ax2+
bx +c6= 0 x
a6= 0 b c ax2+bx +c= 0
x ax3+bx2+cx = 0 x3= 2 x2= (−bx −c)/a
2a+b(−bx−c)/a+cx = 0 x=2a−bc/a
c−b2/a ∗a, b c
x x =3
√2
√2
3
√2
∗c−b2/a 6= 0
c−b2/a = 0 x6= 0 2a−bc/a = 0 c=b2/a
2a3=b3a b
c−b2/a = 0
R
∃x∈R, f(x) = 2x+ 3
∃f:R→R,∀a∈R,∀b∈R,∃x∈R, f(x) = ax +b
y=ax +b x =c
fR∀x∈R, f(x) = x3∀a∈R,∀b∈R,∃x∈
R, f(x) = ax +b a ∈Rb∈RX3−aX −b
x
x3−ax −b= 0 f(x) = ax +b a b

∀f∈E, f ⇔f0
f∈E f f0∀x∈R, f(x) =
f(−x)∀x∈R, f0(x) = −f0(−x)
f0
f∈E f0f∀x∈R, f0(x) =
−f0(−x)h h(x) = f(−x)h
h0(x) = −f0(−x)∀x∈R, f0(x) =
h0(x)
f0=h0(f−h)0= 0 f−h
∃c∈R,∀x∈R, f(x) = h(x) + c∀x∈R, f(x) = f(−x) + c
x= 0 f(0) = f(0) + c c = 0
∀x∈R, f(x) = f(−x)f
∀f∈E, f ⇔f0
f=⇒f0f0=⇒f
∃c∀x∈R, f(x) = −f(−x) + c
c= 0 f
f(x) = x3+ 1 f0(x)=3x2f
∃!f∈E f0=f
f0=f
f0=f
f(x) = λexλ
∀f∈E, ∀g∈E, f =⇒g◦f f ∈E
g◦f x ∈Rg◦f(−x) = g(f(−x)) = g(f(x))
f∀x∈R, g ◦f(−x) = g◦f(−x)g◦f
∀f∈E, ∀g∈E, f =⇒f◦g
f f(x) = x2g g(x) = x+ 1
f◦g(−1) = f(g(−1)) = f(0) = 0 f◦g(1) = f(g(1)) = f(2) = 4 f◦g(−1) 6=f◦g(1)
f◦g
n
n
∃k∈N, k ≥2k2|n n 630

∀k∈N, k|n=⇒k2|n n
n|n
n2|n n2> n
12
∀k∈ P, k|n=⇒k2|n
n
n
∃k∈ P,∃j∈ P, n =kj n
k=j
∀k∈N,∃j∈N, n|k n|(k+j)
j k k +j
k k n k
k
n= 11 k= 18 j= 4
11|18 11|22
∃j∈N,∀k∈N, n|k n|(k+j)j
k
n= 1
j= 0 ∀k∈N,1|k1|k
n= 2 j= 1 ∀k∈N,2|k
2|(k+ 1)
n= 3
n
log10(2)
p∈Zq∈N∗log10(2) = p
qqlog10(2) = p
log10(2q) = p10log10(2) = 10p,2q= 10p= 2p5p
q≥1p≥1
p≥1 5|2p5p5|2q
log10(2)
2q= 2p5p
p=q p = 0 q
n∈N∗k∈0, . . . , n −1n
k+n k+1=n! k!(n−k)! +n! (k+1)!(n−(k+1))! =n!k+1)+(n−k) (k+1)!(n−k)! =
n!n+1
(k+1)!(n+1−(k+1))! =n+1 k+1