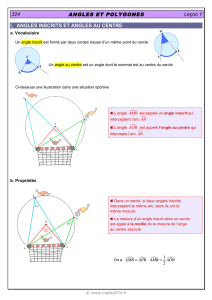
Angles inscrits Angle au centre

Angles inscrits
Angle au centre
Et Polygones réguliers

Objectifs
- Calculer un angle en utilisant la propriété
de l’angle inscrit et de l’angle au centre.
- Construire un polygone régulier.

I. Angles inscrits- angles au centre
1) Introduction et définitions
est un
angle au centre.
BOA ˆ
C’est un angle
dont le sommet
est le centre
du cercle.
BJA 1
ˆ
BJA 2
ˆ
BJA 3
ˆ
, et
sont des angles inscrits.
C’est un angle dont
le sommet est
sur le cercle.

2) Propriétés
En mesurant les angles, on constate que :
BJA 1
ˆ
BJA 2
ˆ
BJA 3
ˆ
mesurent 46°
BOA ˆ
et mesure 92°
Propriété 1
La mesure d’un angle au centre est le double de
celle de l’angle inscrit qui intercepte le même arc.
Propriété 2
Deux angles inscrits qui interceptent
le même arc ont la même mesure.

II. Polygones réguliers
Un polygone régulier est un polygone inscrit dans un cercle
dont tous les côtés ont la même longueur.
O
120°
O90°O
72°
O
45°
O
60°
Triangle
équilatéral Carré Pentagone régulier Hexagone régulier Octogone régulier
Remarques : - Il existe toujours une rotation laissant invariant un
polygone régulier.
-L’angle au centre d’un polygone régulier se calcule avec la
formule suivante angle au centre = 360°
nb côtés polygone