ROTATION - POLYGONES RÉGULIERS O désigne

ROTATION - POLYGONES RÉGULIERS
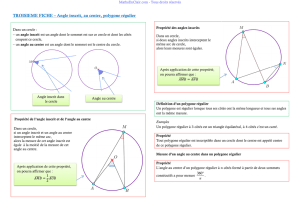
Odésigne un point du plan, Mun point différent
de Oet αla mesure d’un angle en degrés.
L’image M′du point Mpar la rotation de centre O
et d’angle α(dans un sens précisé) est tel que :
•O M ′=OM ;
•
à
M OM ′=αen tenant compte du sens de la rota-
tion ;
O
M
M′
α
Définition
Remarque : Il existe deux sens de rotation :
Ïle sens inverse des aiguilles d’une
montre , encore appelé sens direct ou
positif : ;
Ïle sens des aiguilles d’une montre,
encore appelé sens indirect ou néga-
tif :
Une rotation conserve :
•les distances,
•les aires,
•les angles,
•l’alignement,
•et les milieux ;
Une rotation transforme :
•un segment en un segment,
•une droite en une droite,
•une demi-droite en une demi-droite,
•un cercle en un cercle de même rayon.
Propriétés de conservation
Un polygone régulier est un polygone dont tous les sommets sont sur un même
cercle et dont tous les côtés ont la même longueur.
Définition
Quelques polygones réguliers à connaître :
Le triangle équilatéral Le carré L’hexagone régulier L’octogone régulier
O
120◦
O
90◦
O
60◦
O
45◦
Tous les angles au centre d’un polygone régulier sont égaux. Si nest le nombre
de côtés de ce polygone, alors l’angle au centre est égal à 360
n
Propriété