CHAPITRE 1 : STRUCTURE ALGEBRIQUE 1. Essentiel sur les

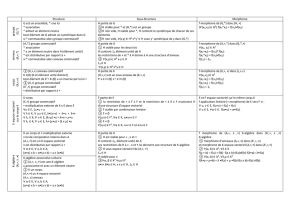
CHAPITRE 1 : STRUCTURE ALGEBRIQUE
1. Essentiel sur les propriétés d’une loi de composition
Soit E ≠ Φ et * une loi de composition définie dans E.
La loi * peut être :
a) Interne et partout définie dans E :
Dans ce cas, l’ensemble E est dit « Stable » par la loi *
b) Associative dans E :
 z)
c) Commutativité dans E :
 x
d) Distributive par rapport à une autre loi Τ définie dans E :
 - x * (y Τ z) = (x * y) Τ (x * z)
Distributive à gauche
-(y * x) Τ (z * x)
Distributive à droite
Exemple :
- L’addition et la multiplication sont des lois de composition internes,
commutatives et associatives dans N, Z, Q et R.
- La multiplication est distributive par rapport à l’addition dans N, Z, Q et
R.
2. Eléments remarquable
Soit E ≠ Φ est * une loi de composition interne dans E. * peut admettre
les éléments remarquable suivants :
a) Elément neutre e :  x = x et e * x = x
b) Eléments symétriques :
Si e est l’élément neutre de * dans E, alors x’ est appelé symétrique de x
dans e. lorsque x Ж x’ = e et x * x’ = e
c) Elément absorbant a :  x * a = a et a * x = a
d) Elément involutif : i * i = e (e le neutre de * dans E)
e) Elément idempotent d : d * d = d
f) Elément simplifiable ou régulier  :
 (x *  = y * ) => (x = y)
( *  =  * y) => (x = y)
Exemple :
- 0 est l’élément neutre pour l’addition dans N, Z, Q et R
- 1 est l’élément neutre pour la multiplication dans N, Z, Q et R
- Le symétrique d’un élément dans Z, Q et R pour l’addition est son
opposé

- Le symétrique d’un réel non nul pour la multiplication est son inverse.
3. Structure de groupe
Soit G ≠ Φ est * une loi de composition définie dans G.
(G, *) est un groupe ssi :
a) * est interne : 
b) * est associative :  z)
c) * Admet un élément neutre :  :  x = x
d) * Admet des éléments symétriques :   :
x * x’ = e et x’ * x = e
Si de plus la loi * est commutative alors (G, *) est un groupe commutatif ou un
groupe abélien.
Exemple :
- (Z, +) ; (Q, +) ; (R, +) ; (Q*, .) et (R*, .) soit des groupes commutatifs
- L’ensemble des homothéties de même centre muni de la loi
(composition des applications) est un groupe abélien.
4. Structure d’anneau et de corps
1) Soit A ≠ Φ, * et Τ deux lois de compositions internes définies dans A.
(A, *, Τ) est un anneau ssi
a) (A, *) est un groupe abélien
b) (A, Τ) est un demi-groupe
c) La loi Τ est distributive par rapport à *
Attention : L’écriture (A, *, Τ) est différente de (A, Τ, *)
Remarque :
- Si (A, Τ) est un demi-groupe unitaire (Τ admet un neutre) alors (A, *, Τ)
est un anneau unitaire
- Si (A, T) est un demi-groupe unitaire commutatif (c'est-à-dire T est
commutatif et admet un neutre) alors (A, *, Τ) est un anneau unitaire
commutatif.
Exemple :
- (Z, +, .) : (Q, +, .) et (P(A), , ∩) sont des anneaux unitaires commutatifs
- ({0}, +, .) est un anneau commutatif.
2) Soit A ≠ Φ : * est T deux lois de composition internes définies dans A.
((A, *, Τ) est un corps ssi
a) (A, *) est un groupe commutatif
b) (A, {e}, T est un groupe (e est le neutre de * dans A)
c) T est distributif par rapport à *.
Si de plus, la loi T est commutatif alors (A, *, Τ) est un corps commutatif ou en
champ.
Exemple :

- (Q, +, .) et (R, +, .)
- (Zn, +, .) est un corps ssi n est premier
- (R², +, .) est un corps commutatif
5. Structure d’espace vectoriel
Soit (R, +, .) un corps commutatif et V est un ensemble non vide.
(V, +, .) est un espace vectoriel sur R ou un R espace vectoriel si :
a) (V, +, .) est un groupe abélien
b) La loi de composition externe . définie de R X V ------> V telle qu’à
tout couple (, ) associe le vecteur  . J vérifie les propriétés
suivantes :
i)       . (  )=  .   +  .   (distributivité de la
multiplication des réels par rapport à l’addition des vecteurs)
ii)        + ) .   =  .   +  .   (distributivité de la
multiplication des vecteurs par rapport à l’addition des réels.
iii)  ,      ) .   =  . ( .  )
(Associativité mixte)
iv)    =   (1 élément neutre de . dans R)
Remarque :
- Les éléments de v sont appelés vecteurs et ceux de corps R des
scalaires
- Tout corps commutatif est un espace vectoriel sur lui-même.
Exemples et contre exemples
- (R, +, *) est un R – espace vectoriel
- (Q, +, *) est un Q – espace vectoriel
- (Q, +, *) n’est pas un R – espace vectoriel
- (R², +, *) est un R – espace vectoriel
- L’ensemble des vecteurs du plan est un R – espace vectoriel.
Questions
1. a) Dans Z, on définit la loi * par :
a * b = a + b + 2
Calculer 2 * 5 ; -11 * 3 ; -1 * -1
b) Dans R0 X R, on définit la loi  par :
(a, b)  c, d) = (ac, bc + d)
Calculer (1, 2)  (3, 4) ; (-
, 1)  (- , - ) ; (a, b)  (a, b)
2. vérifier que la loi T définie dans R\{
} est interne et partout définie.
 R\{
}, x T y = x + y – 2xy

3. Dans l’ensemble K = Q\{-1}, x Q\{-1}, on définit l’opération  par :
(a, b)  (c, d) = (ac + a + c, bd + b + d)
Dans l’hypothèse que (K, ) est un groupe commutatif, déterminer le
symétrique de (-2, 
).
4. On munit l’ensemble R\{-2} des nombres réels de la loi de
composition interne notée * et définie par :
a * b = 2ab + 4(a + b) + 6
Déterminer : a) Le neutre de *
b) Les réels qui sont leurs propres symétriques pour *.
5. Déterminer les éléments idempotents de la loi T définie dans r par :
x T y = xy – 2x – 2y + 1
6. Soit la loi de composition interne * définie dans Q par :
a * b = b + a + ba – 4
Déterminer x sachant que :
(-5 * 
) * x = x * 2
7. Dans Z, on définit les lois * et O par :
a * b = a + b – 3
a O b = ab – 3a – 3b + 12
verifier si O est distributive par rapport à *.
8. Dans R\{1} on définit la loi  par : x  y = 
Déterminer si possible l’élément neutre, le symétrique de -
, les
éléments involutifs et idempotents
9. On considère les lois * et T définies dans Q par :
a * b = 2ab et a T b = a + 2ab
On peut vérifier que * confère à Q* la structure de groupe
commutatif et que (Q, T, *) est un anneau commutatif.
a) Résoudre le système 1 * x * 
 = 1
 * x *   = 2
Et déterminer le rapport 1 
b) Calculer la valeur numérique de x sachant que
X =  
10. Pourquoi (Q, +, .) n’est pas un espace vectoriel sur R.