ue 4 analyse descriptive univariee d un echantillon statistique

Analyse descriptive univariée d'un échantillon statistique
I. Introduction
•Plan classique d'une étude :
◦Recueil des données (libre observation ou expérience).
◦Analyse descriptive des données.
◦Inférence statistique (recherche d'associations, prédiction...).
•Plusieurs type de variables (cf plan) :
◦Qualitatives.
▪Non ordonnées.
▪Ordonnées.
◦Quantitatives.
▪Discrètes.
▪Continues.
◦Cas particuliers.
▪Binaires.
▪Rangs.
•Pour chacun de ces types nous verrons.
◦Définition.
◦Présentation des données.
◦Représentation graphique.
◦Calculs des paramètres.
II. Variables qualitatives non ordonnées
A. Définition
•Variable non quantifiable décrivant une qualité d'un individu à l'aide de k modalités.
•Les modalités forment donc un S.C.E. (système complet d’événements).
•Variable « nominale » si k > 2.
•Exemple : couleur des cheveux.
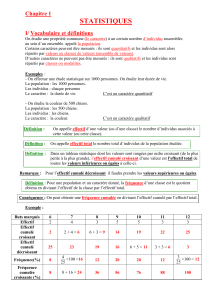
B. Présentation des données
•Tableau de contingence.
•Une ligne pour chacune des k modalités (i de 1 à k).
Modalité Effectif Fréquence
xinifi=ni/N
Σ = N Σ = N
brun blond blanc Ensemble S

C. Représentation graphique
•Diagramme en secteur = camembert.
•Proportionnalité entre :
◦La fréquence fi.
◦L'effectif ni.
◦L'angle au centre (en degrés : α = 360°*fi).
◦La surface du secteur.
D. Calcul de paramètres
•Un seul paramètre : le mode.
•Mode = modalité ayant le plus grand effectif.
Exercice 1.
◦Couleur des cheveux chez cents individus.
Couleur xinifi
Bruns 50 0,5
Blonds 30 0,3
Blancs 20 0,2
Σ=N=100 Σ=1
Mode = ''bruns''.
III. Variables qualitatives ordonnées = variables ordinales
•Les modalités ont un ordre.
Variable = niveau d'étude
Brevet
Bac
Licence
Master
•Comportement identique aux variables nominales.
•Tableau : on peut trier les lignes par x croissants, ajouter l'effectif cumulé et calculer la
médiane (cf. post).
Brun
0,5
Blanc
0,2
Blond
0,3

IV. Variables quantitatives discrètes
A. Définition
•Variable numérique ne pouvant prendre qu'un nombre fini de valeurs.
•Souvent issues d'un décompte.
•Exemple.
◦Nombre d'enfants dans une famille.
◦Nombre de rechutes d'une maladie.
B. Présentation des données
•Tableau de contingence.
•Une ligne pour chacune des k valeurs différentes triées de X (i de 1 à k).
Modalité Effectif Effectif cumulé Fréquence Fréquence
cumulée
xiniNi = Σ nj fi=ni/N Fi = Σ fj
xknkN fk1
Σ = N Ø Σ = 1 Ø
•cf Exercice 2A.
C. Représentation graphique
1. Représentation graphique
•Rappels préalables, cas discret.
◦f(x) est la densité de probabilité de X.
▪f(x0) = P(X=x0)
▪ x, 0 ∀≤ f(x)≤ 1
▪∑ f(xi) =1
◦F(x) est la fonction de répartition de X.
▪F(x0) = P(X=x0)
◦F(x) est la primitive de f(x) qui vérifie 3 propriétés.
▪F(x) croissante sur ]-∞;+∞[
▪Lim x→-∞ F(X) = 0
▪Lim x → +∞ F(X) = 1
2. Diagramme en bâtons
•Diagramme en bâtons.
•Polygone des effectifs.
•Attention :
◦Interdiction d'élargir les barres.
◦Échelle réellement quantitative en X.
◦Polygone en pointillés.
j=1
i
j=
1
i
i=1
k

3.Diagramme cumulatif
•Diagramme cumulatif (en fréquences).
•Fournit la médiane graphiquement (cf. exercice).
•Schéma.
◦Y : fréquence cumulée.
•cf Exercice 2B.
D. Calcul des paramètres
•Paramètres calculables.
◦Minimum, maximum.
◦Mode (idem qualitatif).
◦Médiane.
◦Quantiles. cf. ci-après
◦Moyenne, variance et écart type.
1. Médiane
•Médiane x :
◦Valeur seuil qui partage l'échantillon en 2 sous-groupes d'effectif identique.
▪Si N impair : soit N=2p+1, médiane = xp+1
▪Si N pair : soit N=2p, médiane = (xp+xp+1)/2
◦Robuste aux valeurs extrêmes.
2. Quantiles
•Quartiles.
◦Les 3 valeurs qui partagent l'échantillon en 4 sous-groupes d'effectif identique.
◦Distance inter-quartile = Q3-Q1
◦Médiane = Q2 (2e quartile).
Fi
fj
XiXjX
Polygone des
effectifs => Estimation graphique de F(x).
1
Fj
Fi
0
XiXjX
~

•Percentiles.
◦Les 99 valeurs qui partagent l'échantillon en 100 sous-groupes d'effectif identique
◦Médiane = 50ème percentile.
•Quantiles.
◦Terme générique.
3. Moyenne
•La moyenne arithmétique.
▪x =E(x)= ∑ xifi
•Contrairement à la médiane.
◦Sensible aux valeurs extrêmes.
◦Nombreux tests et calculs réalisables.
•En moyenne, les écarts à la moyenne sont nuls
◦E (x-x) = ∑ (xi-x) . fi = 0
4. Variance et écart type
•Variance et écart type en théorie...
◦Variance σ2 = E [(x-x)2]
= Σ (x-x)2 .fi
σ2 = E(X2) – [E(X)]2= ( ∑ xi2. fi) - (∑ xi fi)2
•Écart type σ= √(σ²)
•Variance et écart type en pratique sur un échantillon (cf. cours suivant).
◦Estimateur biaisé de l'écart type.
Sech se calcule comme σ mais sur l'échantillon.
◦s =Estimateur non biaisé de l'écart type.
=ds (déviation standard).
=sd (standard deviation).
S = Sech √ N / (N – 1)
Q1Q2Q3
x
0
0,25
0,5
0,75
1
Distance inter-quartile
i=1
k
i=1
k
i=1
k
i=1
k
i=1
k