Chapitre 2 : Variables aléatoires et distributions I. Définitions et exemples Définition 1

Chapitre 2 : Variables aléatoires
et distributions
I. Définitions et exemples
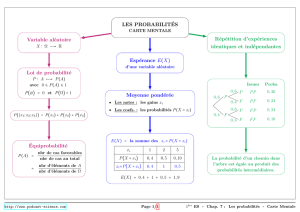
Définition 1 Etant donnée une expérience aléatoire
(Ω,F,P). Une variable aléatoire Xest une quantité
dont la valeur dépend du résultat de l’expérience
aléatoire. Xest une application de
Ω−→ R
ω7−→ X(ω)
telle que ∀B⊂R
{ω∈Ω|X(ω)∈B}∈F
Probabilités– A. YAACOUBI – Novembre 2011 – p. 1/44

Probabilités– A. YAACOUBI – Novembre 2011 – p. 2/44

Exemples
Exemple 1 : Lancer une pièce de monnaie.
X(P) = 1 et X(F) = 0
Exemple 2 : Lancer un Dè équilibré.
X(k) = √k
Exemple 3 : Lancer deux Dès équilibrés.
X((i, j)) = i+j
Exemple 4 : Choisir un pointMau hasard de façon
uniforme sur un disque de centre O et de rayon R.
X=distance de MàO
Probabilités– A. YAACOUBI – Novembre 2011 – p. 3/44

II-Loi ou distribution d’une va-
riable aléatoire
II.1-Le cas discret :
Définition 2 Une variable aléatoire X est dite
discrète si l’ensemble de ses valeurs possibles E
est ou bien un ensemble fini, ou bien un ensemble
infini dénombrable.
Dans ce cas on définit la loi de Xpar
p(x) = P{X=x}=P{ω∈Ω|X(ω) = x}
l’application : p:E−→ [0,1] ainsi définie
S’appelle fonction de masse de la v.a.r X
Probabilités– A. YAACOUBI – Novembre 2011 – p. 4/44

Fonction de masse
Exemple 3 Lancer d’une pièce de monnaie
p(1) = P{X= 1}=P{P}= 1/2
et
p(0) = P{X= 1}=P{F}= 1/2
Exemple 4 Lancer deux Dès équilibrés.
X(ω) = la somme des deux résultats.
E={2,3,4,5,6,7,8,9,10,11,12}
X2 3 4 5 6 7 8 9 10 11 12
p(x)1
36
2
36
3
36
4
36
5
36
6
36
5
36
4
36
3
36
2
36
1
36
Probabilités– A. YAACOUBI – Novembre 2011 – p. 5/44