3 Fonctions polynômes

3 Fonctions polynômes
3.1 Fonction polynôme de degré n
Définition : Une fonction polynôme est une fonction de la forme :
f(x) = anxn+an−1xn−1+...+a2x2+a1x+a0=
i=n
X
i=0
aixi
Si nest le plus grand exposant des puissances de xon dit que la fonction polynôme est de
degré n.
Exemples :•f(x) = 3x5−4x3+x2+ 3 est une fonction polynôme de degré 5.
•f(x) = x2−6x+ 9 est une fonction polynôme de degré 2 ; on parle aussi de trinôme.
Propriétés :•Soit fla fonction définie par f(x) = xn, avec n > 0, alors fest dérivable sur
Ret sa fonction dérivée est f′(x) = nxn−1.
•La dérivée d’une fonction constante f(x) = k, où k∈R, est f′(x) = 0.
Cas particulier : Si n= 1 la fonction f(x) = xnest la fonction f(x) = xet sa dérivée est,
d’après la propriété ci-dessus : f′(x) = 1 ×x1−1=x0= 1.
3.2 Opérations sur les dérivée
Propriétés :•Soit uune fonction définie sur un intervalle Iet k∈R. Si la fonction uadmet
une fonction dérivée u′sur l’intervalle I, alors la fonction fdéfinie par f(x) = ku(x) est
dérivable sur Iet sa fonction dérivée est f′(x) = ku′(x).
•Soient uet vdeux fonctions définies sur un intervalle I. Si uet vadmettent pour fonctions
dérivées respectives u′et v′sur I, alors la fonction fdéfinie par f(x) = u(x) + v(x) est
dérivable sur Iet sa fonction dérivée est : f′(x) = u′(x) + v′(x)
(la dérivée d’une somme est la somme des dérivées).
Exemples :•La fonction f(x) = 5x7est définie et dérivable sur R. En effet fest le produit de
5 par la fonction u(x) = x7, de dérivée u′(x) = 7x6, d’où f′(x) = 5 ×7x6= 35x6.
•La fonction f(x) = x4+xest la somme des fonctions u(x) = x4et v(x) = x, alors la dérivée
de la fonction fest f′(x) = u′(x) + v′(x) = 4x3+ 1.
3.3 Étude des variations d’une fonction
Les propriétés précédentes permettent de calculer la fonction dérivée d’une fonction polynôme.
7

Maths Tstmg 3. Fonctions polynômes prog 2011
Exemple :f(x) = 5x4−8x3+ 4x2−3x−7. On calcule la dérivée f′de fen écrivant la somme
des dérivée de chaque fonction composant f:f′(x) = 5 ×4x3−8×3x2+ 4 ×2x−3 + 0 =
20x3−24x2+ 8x−3.
Propriété : Soit fune fonction définie sur un intervalle I, alors fest dérivable sur Iet
l’étude du signe de la dérivée permet d’affirmer que :
— si pour tout x∈Ion a f′(x)>0, alors fest croissante sur I;
— si pour tout x∈Ion a f′(x)60, alors fest décroissante sur I.
Exemple : Soit f(x) = x4+ 4x3−7. La fonction fest définie et dérivable sur Ret f′(x) =
4x3+ 12x2, d’où, en factorisant l’expression de f′, on obtient : f′(x) = 4x2(x+ 3) ; ceci permet
d’étudier le signe de f′et par suite les variations de f:
x−∞ −3 0 +∞
x+ 3 −0 + 3 +
4x2+ 36 + 0 +
f′(x)−0 + 0 +
f(x)−34 −7
3.4 Tangente à la courbe en un point
Définition : Si fest dérivable en a, on appelle tangente en A(a;f(a)) à la courbe Cf, la
droite qui passe par Aet qui a pour coefficient directeur le nombre dérivé f′(a).
x
y
A
−1
2
y= 2x−5
0
Cf
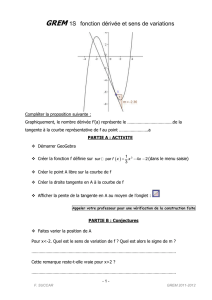
Exemple : Soit la fonction polynôme f(x) = x3−3x2+ 2x−1.
On veut déterminer l’équation de la tangente à la courbe re-
présentative de la fonction fau point d’abscisse 2.
f′(x) = 3x2−6x+ 2, donc f′(2) = 3 ×4−6×2 + 2 = 2 et
f(2) = 8 −3×4 + 2 ×2−1 = −1.
Le coefficient directeur de la tangente à la courbe Cfau point
A(2; −1) est f′(2) = 2, donc son équation est de la forme :
y= 2x+b. Pour déterminer l’ordonnée à l’origine b, il suffit
d’écrire que le point A(2; −1) appartient à la tangente, soit :
−1 = 2 ×2 + b, d’où b=−5 et l’équation de la tangente est :
y= 2x−5.
Théorème : Si fest dérivable en a, alors une équation de la tangente àCfen A(a;f(a)) est
y=f′(a)×(x−a) + f(a).
Exemple : Pour la fonction polynôme précédente : f′(2) = 2 et f(2) = −1, donc l’équation de
la tangente est : y= 2(x−2) −1, soit y= 2x−5.
math4
bac – 8 – v1.618