Document

MATHEMATIQUES
Exemples de calculs
En trigonométrie
Classe de 3ème
Document1 1/3 fg
Exemple 1 : Calculer 
,
à 1° près.
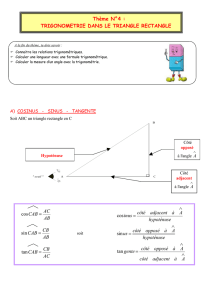
On sait que le triangle ABC est rectangle
en A. On cherche l’angle 
 on connaît
son côté opposé et l’hypoténuse.
On applique la définition du sinus :
On remplace :  
On utilise la calculatrice (  et on
trouve 
Exemple 2 : Calculer 
On sait que le triangle ABC est rectangle
en A. On cherche l’angle 
 on connaît
son côté adjacent et l’hypoténuse.
On applique la définition du cosinus :
On remplace :  
On utilise la calculatrice (  et on
trouve 
Exemple 3 : Calculer AC
à 0,1 près
On sait que le triangle ABC est rectangle
en A. On connaît l’angle 
 on cherche
son côté adjacent et on connaît
l’hypoténuse.
On applique la définition du sinus :
On remplace :   
Donc

MATHEMATIQUES
Exemples de calculs
En trigonométrie
Classe de 3ème
Document1 2/3 fg
Exemple 4 : Calculer AB à 0,1 près.
On sait que le triangle ABC est rectangle
en A. On connaît l’angle 
 on cherche
son côté adjacent et on connaît
l’hypoténuse.
On applique la définition du cosinus :
On remplace :   
Donc     
Exemple 5 : Calculer BC
à 0,01 près
On sait que le triangle ABC est rectangle
en A. On connaît l’angle 
 on cherche
l’hypoténuse et on connaît le côté adjacent.
On applique la définition du cosinus :
On remplace :   
Donc 
Exemple 6 : Calculer BC à  près
On sait que le triangle ABC est rectangle
en A. On connaît l’angle 
 on cherche
l’hypoténuse et on connaît le côté opposé.
On applique la définition du sinus :
On remplace :   
Donc 

MATHEMATIQUES
Exemples de calculs
En trigonométrie
Classe de 3ème
Document1 3/3 fg
Exemple 7 : Calculer AC
à  près
On sait que le triangle ABC est rectangle
en A. On connaît l’angle 
 on cherche
son côté opposé et on connaît son côté
adjacent.
On applique la définition de la tangente:
On remplace :   
Donc      