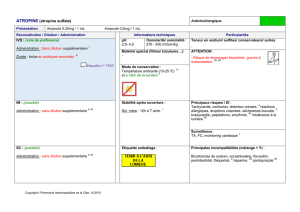
Sadiki Vendredi 7 -3-2008 4ème maths Devoir de synthèse n° : 2

1/
Collège Sadiki
Devoir de synthèse n° : 2
Sciences physiques
4ème maths
Vendredi 7 -3-2008
Profs : Obey- Fkih et Cherchari
 On donnera l’expression littérale avant de passer à l’application numérique.
 L’utilisation de la calculatrice non programmable est autorisée.
 Numéroter les questions.
Exercice 1 : (2,5 pts) :
On considère la réaction de synthèse de l’ammoniac (NH3)
N2 + 3H2 
 2NH3
1) Dans une enceinte de volume V=1,3 L et à une température T, on introduit a moles de
diazote et b moles de dihydrogène. A l’équilibre dynamique, on obtient un mélange gazeux
contenant 0,8 mole d’ammoniac, 3 moles de H2 et 1 mole de N2.
Calculer a et b.
2) Le système précédent étant en état d’équilibre. Préciser, en le justifiant, l’influence sur
l’équilibre suite à :
a- Une augmentation de pression à température constante.
b- Un ajout de a moles de NH3 à température et à volume constants.
c- Une diminution de température à pression constante, sachant que la réaction de
dissociation de l’ammoniac est endothermique.
Exercice 2 : (4,5 pts) :
Soit un monoacide AH en solution aqueuse diluée, de concentration molaire C.
1) a) Ecrire l’équation chimique de la réaction de l’acide avec l’eau.
b) Dresser le tableau d’avancement (en utilisant l’avancement volumique y).
c) Exprimer le taux d’avancement final de la réaction de dissolution de l’acide en fonction de
son pH et de sa concentration molaire initiale C.
2) Le tableau suivant comporte les renseignements concernant deux solutions aqueuses diluées (S1)
et (S2) d’acides respectifs A1H et A2H et de même concentration molaire.
A1H
A2H
pKa1
pKa2
C1=3.10-2 mol.L-1
C2= C1
pH1=3,10
pH2=2,9
a- Calculer le taux d’avancement final de la réaction de dissolution de chaque acide dans l’eau.
b- Montrer que les deux acides sont faibles. Préciser, en le justifiant, l’acide le plus fort.
c- Comparer pKa1 et pKa2.
d- Calculer pKa2 sachant que A2H est faiblement ionisé et que son pH =
 (pKa2 – logC).
3) Un prélèvement de volume V2=10 mL de la solution (S2) est soumis à une dilution au
dixième, on obtient ainsi une nouvelle solution S’2 ayant un pH=pH’2. Voila la liste de
matériel pouvant être utile à la dilution : fiole jaugée de 50 mL ; fiole jaugée de 100
mL ; pipette à deux traits de jauge de 10mL ; pipette à deux traits de jauge de 5mL ; de
l’eau distillée.
a) Décrire la démarche expérimentale à suivre, en précisant le matériel choisi parmi << matériel pouvant
être utile à la dilution >>, pour effectuer une dilution au dixième.
b) Calculer la valeur de pH’2. Déduire le taux d’avancement final après dilution.
c) Comparer le taux d’avancement final de la réaction de dissolution de l’acide A2H avant et après dilution.
Conclure.
Chimie ( 7 points )

2/
Exercice 1 : (6,5 pts) :
Un solide (S) de masse m est attaché à
l’extrémité d’un ressort à spires non jointives de masse négligeable et
de raideur K=20 N.m-1, l’autre extrémité du ressort est attachée à
un point fixe. Le système S0={ (S) + ressort} est placé sur un plan
horizontal (figure 1). Au repos, le centre d’inertie G du solide est au
point O, origine d’un repère (O,i) horizontal. A partir de O,
on écarte le solide (S) d’une distance Xm dans le sens
positif et on le lâche sans vitesse.
A- Les frottements sont négligeables.
1) a- Représenter les forces exercées sur le solide (S)
en mouvement à une date t quelconque.
b- Etablir l’équation différentielle du mouvement et
déduire l’expression de la pulsation propre 0 de
l’oscillateur.
c- On donne le graphe représentant les variations
de l’accélération du solide (S) en fonction de
l’élongation x (figure 2). Déterminer
graphiquement 0. Montrer que la masse du
solide est m=200 g.
2) a- Au passage du solide (S) par une position
d’abscisse x sa vitesse est v, donner l’expression de
l’énergie mécanique totale E du système S0 en
fonction de m, v, K et x.
b- Montrer que l’énergie E est constante puis
l’exprimer en fonction de K et Xm.
3) On donne le graphe qui représente les variations de
l’énergie cinétique Ec du solide en fonction du temps
(figure 3). La loi horaire du mouvement est donnée par x(t)=Xmsin(0t+)
a- Montrer que l’énergie cinétique Ec s’écrit sous la forme Ec=1/4KX2m(1+ cos(20t+ 2).
b- A partir du graphe, déduire les valeurs de Xm et  puis écrire, en fonction du temps, la loi
horaire du mouvement.
B- Les frottements ne sont plus négligeables.
Le solide (S) est maintenant soumis à une force de frottement visqueux f=-hv (h=cte>0), le
graphe de la figure 4 représente les variations de son abscisse x en fonction du temps. ( les
conditions initiales sont les mêmes que dans la partie A).
1) Etablir l’équation différentielle du mouvement de (S) en fonction de son abscisse x.
2) Montrer que l’énergie totale du système S0 diminue au cours du temps.
3) Sachant que la variation de l’énergie totale du système S0 est égale au travail de la force de
frottement, calculer ce travail entre les dates t1 et t2.
Physique ( 13 points )
Fig.
5
i
O
(S)
(R)
x
Fig 1
0
3
-
3-
-
-
dx
dt (m.s-2)
x(10-2 m)
Fig2
Ec(10-3 J)
t(s)
9
4,5
0
Fig 3

3/
Exercice 2 : (6,5 pts)
Un pendule élastique est constitué d’un solide (S) de masse m=0,2 Kg attaché à l’extrémité d’un
ressort (R) à spires non jointives de masse négligeable et de raideur K, l’autre extrémité du ressort
est fixe. Le pendule repose sur un plan horizontal (figure 1) et la position du centre d’inertie G du
solide est repérée sur un axe horizontal (O,i), d’origine O position d’équilibre du solide. Au cours de
son mouvement, le solide (S) est soumis à une force de frottement visqueux f=-hv (h=1,5 Kg.s-1).
Un dispositif approprié exerce sur (S) une force excitatrice F=Fmsin(t).i, d’amplitude Fm constante
et de pulsation  réglable.
1) Comment peut-on montrer expérimentalement que les oscillations du solide (S) sont forcées ?
2) Etablir l’équation différentielle du mouvement.
3) La solution de l’équation différentielle précédente est x(t) =Xmsin(t + )
a- Faire la construction de Fresnel dans le cas ou <0 (0 pulsation propre de l’oscillateur).
b- Déduire l’expression de l’amplitude Xm en fonction de K, m, h,  et Fm ainsi que celle de
tg.
4) Expliquer brièvement la résonance d’élongation et donner l’expression de la pulsation r
correspondante en fonction de 0, h et m.
5) a- Donner l’expression de l’amplitude Im de l’intensité du courant i(t) traversant un circuit
RLC en régime sinusoïdal forcé en fonction de R, L, , C et Um.
b- Déduire, en précisant l’analogie utilisée, l’expression de l’amplitude Vm de la vitesse du
solide (S) en fonction de h, m, , k et Fm.
c- Montrer que l’impédance mécanique s’écrit sous la forme Zméc = h  m k
.
6- Pour une valeur 1=20 rad.s-1 de la pulsation de l’excitateur, l’impédance mécanique est
minimale et égale à h alors que l’amplitude Xm a pris la valeur 8 cm.
a- Montrer que le pendule élastique est à la résonance de vitesse. Calculer K et Fm.
b- Déduire la valeur de  dans ces conditions.
c- Tracer l’allure de la courbe représentant Zméc =f() en précisant le point correspondant
à (Zméc )min.
x(cm)
t
t1
2,8
t1
-2,2
Fig 4