Oscillations électriques forcées Série physique 10

Oscillations électriques forcées
Série physique 10
Site web : http://cherchari.legtux.org / Facebook : https://www.facebook.com/mhamed.cherchari
Cherchari
A- Exercices de synthèse :
Exercice n° : 1
Un dipôle AB comprend en série :
- Une bobine d’inductance L=0,20 H et de résistance r inconnue.
- Un résistor de résistance R=80 Ω.
- Un condensateur de capacité inconnue C.
Le dipôle AB est branché aux bornes d’un générateur BF délivrant une tension alternative sinusoïdale
u(t)=Umsin(t ) de fréquence N réglable. Un voltmètre est
branché aux bornes du GBF indique une tension constante U.
L'équation reliant i(t), sa dérivée première
dt)t(di
et sa primitive
idt
est :
(R+ r)i(t) +L
dt)t(di
+
C
1
idt
= u(t)
A l’aide d’un oscilloscope bicourbe, on visualise les tensions
u(t) et uR(t) aux bornes du résistor.
La sensibilité horizontale est égale à 5 ms.div-1 .
La sensibilité verticale de la voie 1 est 5 V.div-1.
La sensibilité verticale de la voie 2 est 1 V.div-1.
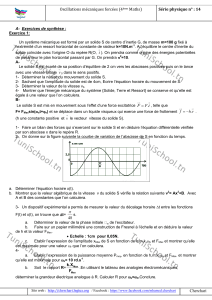
1- Pour une valeur N1 de la fréquence, on obtient
l’oscillogramme de la figure 1
a- En tenant compte des sensibilités verticales, identifier les tensions visualisées respectivement sur la voie
1 et sur la voie 2. Calculer la pulsation 1 et la tension efficace UR aux bornes du résistor.
b- Faire le schéma du circuit en précisant les connexions à l’oscilloscope.
c- Calculer le déphasage angulaire de la tension u(t) par rapport à l’intensité i(t), =u - i. Calculer i. Le
circuit est résistif, capacitif ou inductif.
d- Calculer l’intensité efficace I du courant traversant
le circuit. Calculer l’impédance Z du dipôle AB.
2- a- Faire la construction de Fresnel.
Echelle : 1V → 1cm
b-Déduire les valeurs de r et C.
3- En faisant varier C ou , on obtient l’oscillogramme
de la figure 2. La sensibilité verticale de la voie
2 est maintenant 2V.div-1
a- Quel est l’état du circuit ? Justifier la réponse.
b- Quel paramètre a-t on modifié ? Calculer sa
nouvelle valeur.
c- Etablir l’expression de l’intensité en fonction du
temps.
d- Y’a-t-il surtension dans ces conditions ?
Calculer la puissance moyenne consommée par le circuit RLC.
Exercice n°2 :
Le circuit de la figure -1- à remplir par le candidat et à remettre avec la copie comporte :
- un résistor de résistance R = 24 ,
- un condensateur de capacité C ,
- une bobine d’inductance L = 0,8 H et de résistance interne r .
L’ensemble est alimenté par un générateur basse fréquence (G.B.F.) délivrant une tension
sinusoïdale u(t) =
Um.sin(2.N.t) telle que Um
est constante et égale à
10 V et la fréquence N est
réglable.
L’intensité instantanée du
courant électrique est i(t) =
I
2
sin(2.N.t + i) .
Fig 2
u(v)
t(s)
Fig 1
Voie 1
Voie 2
figure -1-

Oscillations électriques forcées
Série physique 10
Site web : http://cherchari.legtux.org / Facebook : https://www.facebook.com/mhamed.cherchari
Cherchari
1°) Un oscilloscope bicourbe permet de visualiser sur la voie (Y1) la tension u(t) et sur la voie (Y2) la
tension uR(t) aux bornes du résistor .
Indiquer , sur la figure -1- à remplir par le candidat et à remettre avec la copie , les connexions
nécessaires
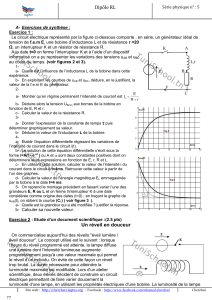
2°) Quand la fréquence N est ajustée à la valeur 202 Hz , sur l'écran de l'oscilloscope on observe les
deux courbes (1) et (2) de la figure -2-
a) Identifier les courbes (1) et (2) et en déduire si
le circuit est inductif , capacitif ou équivalent à une
résistance pure
b) Déterminer les valeurs de I et de i .
3°) L'équation différentielle reliant i(t) , sa dérivée
première
dt)t(di
et sa primitive
idt
s'écrit :
Ri(t) + ri(t) + L
dt)t(di
+
C
1
idt
= u(t) .
La construction de Fresnel correspondant à la
fréquence N = 202 HZ est donnée par la figure -3
-
où l'échelle adoptée est : 1 cm
2
2
Volt . Dans
cette figure :
- le vecteur
ON
est associé à la tension u(t) .
- le vecteur
OM
est associé à la tension uR(t)
.
- le vecteur
MN
est associé à la tension aux bornes de l'ensemble { bobine, condensateur } .
Déduire de cette construction de Fresnel la valeur de r et celle de C.
4°) On agit sur la fréquence N du (G.B.F.) tout en gardant Um constante, de manière à rendre les deux
courbes correspondant aux tensions u(t) et UR(t) en phase.
a) Quel est le phénomène observé ?
b) Préciser , en le justifiant , si l'on doit augmenter la valeur de N ou la diminuer pour atteindre cet objectif.
c) Montrer que le circuit se comporte dans ces conditions comme un circuit LC. Calculer son énergie totale.
figure -3-
1 cm
2
2
Volt
Fig 2
98

Oscillations électriques forcées
Série physique 10
Site web : http://cherchari.legtux.org / Facebook : https://www.facebook.com/mhamed.cherchari
Cherchari
d) Représenter, sans souci d’échelle, la tension u(t) aux bornes du générateur et uc(t) aux bornes du
condensateur.
e) caculer la puissance moyenne du circuit.
f) y’a t-il surtension ?
B- exercice bac
99
1
/
5
100%