OSCILLATIONS DANS UN CIRCUIT SERIE R.L.C BUT : Etude des

__________________________________________________________________________________________
0scillations circuit RLC-1
Plate-forme 3E (Électricité, Electronique, Electrotechnique). – Université J.Fourier Grenoble
OSCILLATIONS DANS UN CIRCUIT SERIE R.L.C
BUT : Etude des deux régimes d'oscillation dans un système modèle :
- oscillations libres pour différents amortissements dans un régime pseudo-periodique; transition
vers le regime aperiodique.
- oscillations forcées en régime stationnaire. Caractérisation de la résonance pour différents
amortissements. Facteur de qualité.
MATERIEL : on dispose d'un générateur de signal de fréquence variable, d'une bobine a noyau de
ferrite d'inductance l=1H, d'un condensateur de capacité c=0.1µ Fet d'une série de résistances
variables (boites AOIP. on alimentera le circuit rlc avec la borne "out" du générateur. vous disposez
aussi d'un oscilloscope pour la mesure de la variation temporelle du signal électrique et d'un
fréquencemètre.
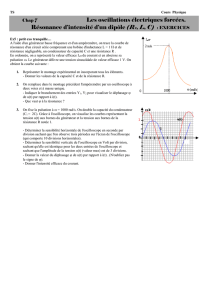
R
L , R
L
C
V
C
(t)
I(t)
V
génerateur
r
1 - Oscillations libres
On s'intéresse aux oscillations libres de la tension aux bornes du condensateur VC (t). Calculer la
période propre T0 et la résistance critique RC du circuit.
Rappel : La résistance critique est la résistance qui donne un amortissement σ = ω0 (régime
critique).
Réaliser le circuit schématisé ci-dessus. On alimente le circuit par un créneau de période ≅ 20⋅T0.
(pour stabiliser le signal à l'écran de l'oscilloscope, on peut utiliser la sortie "TTL" du générateur
pour synchroniser la base de temps de l'oscilloscope "EXT").
Que voit-on à l'oscilloscope ? Pourquoi a-t-on utilisé un signal en créneau (et pas sinusoïdal ou
triangulaire) ? Quelle est l'excitation analogue dans le cas de l'oscillateur mécanique ?
Mesurer δ et la pseudo-période T pour deux valeurs de la résistance R = 10 Ω et R = 1000 Ω.
Comparer δ à sa valeur théorique. Pour le calcul de σ doit-on prendre en compte la résistance de la
bobine (RL ) et la résistance interne du générateur (r)?
Comparer T à T0 et expliquer le résultat.
Augmenter progressivement R pour obtenir le régime critique. Avec quelle précision mesure-t-on
Rc ? Comparer à la valeur théorique.
2 - Oscillations forcées, résonance série
On alimente le circuit précédent avec une tension sinusoïdale.
Dans ce qui suit, on négligera le régime transitoire et on supposera que l'on est en régime
stationnaire. Pourquoi ? (estimer l'ordre de grandeur de la constante de temps τ ).
Pour R = 1000 Ω et pour une fréquence d'excitation ω = ω0 /2 , effectuer la construction de Fresnel
pour déterminer l'impédance du circuit RLC.
Lorsque ω = ω0 , définir Z, ϕ, VL, VC. Donner l'expression du facteur de qualité Q.

__________________________________________________________________________________________
0scillations circuit RLC-2
Plate-forme 3E (Électricité, Electronique, Electrotechnique). – Université J.Fourier Grenoble
Exprimer algébriquement l'impédance complexe Z du circuit. En déduire l'expression du courant I
et de la tension aux bornes du condensateur VC (on considère Vgénérateur connue et constante).
Déterminer pour quelles valeurs de ω, I et VC sont maximales (résonance de courant et/ou de
tension)? Dans quelles conditions ces deux résonances deviennent très proches?
Réaliser les montages permettant de tracer les courbes VC (ω) et ensuite I(ω) en fonction de la
fréquence pour R = 10 Ω et pour R = 1000 Ω . Maintenir la tension aux bornes du circuit
constante (≅ 3 V) quand on fait varier la fréquence.
Comparer sur le même graphe les caractéristiques (fréquence de résonance, amplitude et largeur)
des deux courbes I(ω) et sur un autre VC (ω). Interpréter ces résultats.
Calculer le facteur de qualité par différentes méthodes (voir partie théorique). Comparer leurs
précisions. Conclusions. ( Présenter ces résultats sous forme de tableau ).