Ch4 : Écriture fractionnaire 1 Multiples et diviseurs 2 Fraction et

Ch4 : Écriture fractionnaire
5e
Objectifs
• Ramener une division dont le diviseur est décimal à une division
dont le diviseur est entier.
• Reconnaître, dans des cas simples, si un nombre entier positif est
multiple ou diviseur d’un autre nombre entier positif.
1
• Utiliser l’écriture fractionnaire comme expression d’une proportion, d’une fréquence.
• Utiliser sur des exemples numériques des égalités du type ac
= ab .
bc
Multiples et diviseurs
Définition (Multiple, diviseur)
Soient a et b deux nombres entiers positifs. Lorsque le reste de la division de a par b est égal à zéro, on dit que a est
un multiple de b, ou que b est un diviseur de a, ou encore que a est divisible par b.
Exemple : 15 est un multiple de 3 car 15 = 3 × 5. Autrement dit, 3 est un diviseur de 15, ou 15 est divisible par 3.
17 n’est pas un multiple de 3, car 17 = 3 × 5 + 2.
Règle (Critères de divisibilité)
Pour savoir si un nombre donné est divisible par 2, 3, 5, 9 ou 10, on utilise les critères suivants :
• Un nombre sera divisible par 2 s’il se termine par 0, 2, 4, 6 ou 8.
• Un nombre sera divisible par 3 si la somme de ses chiffres est un multiple de 3.
• Un nombre sera divisible par 5 s’il se termine par 0 ou 5.
• Un nombre sera divisible par 9 si la somme de ses chiffres est un multiple de 9.
Exemple : Le nombre 1380
– est divisible par 2, car il se termine par le chiffre 0.
– est divisible par 3, car 1 + 3 + 8 + 0 = 12 qui est un multiple de 3.
– est divisible par 5, car il se termine par le chiffre 0.
– n’est pas divisible par 9, car 1 + 3 + 8 + 0 = 12 qui n’est pas un multiple de 9.
2
Fraction et proportion
Règle
À une fraction
a
a
, on fait correspondre le quotient a ÷ b : = a ÷ b.
b
b
2
Exemple :
= 2 ÷ 5 = 0, 4.
5
3
= 3 ÷ 7 ≈ 0, 428 471 · · ·.
7
Définition (Fraction)
Une fraction indique quelle partie d’un tout on doit prendre.
2
Exemple : Une tarte pèse 600 grammes. Combien pèse de la tarte ?
5
600 × 2 ÷ 5 = 240 g.
3
Simplification
Règle
Si on multiplie ou divise le numérateur et le dénominateur d’une fraction par un même nombre non nul, on obtient
a×k
a
.
une fraction égale à la fraction initiale : =
b
b×k
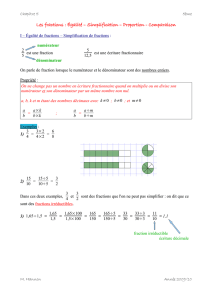
Exemple :
2×2
2
4
=
= .
6
3×2
3
Pour simplifier au maximum une fraction, on applique la règle précédente afin d’obtenir le numérateur et le dénominateur
les plus simples possible. On obtient alors une fraction irréductible.
Ch4 : Écriture fractionnaire
4
a.
5e
Comparaison de fractions
Comparaison de fractions ayant le même dénominateur
Règle
Pour comparer deux fractions ayant le même dénominateur, il suffit de comparer les numérateurs : la fraction ayant
le plus grand numérateur est la plus grande.
4
3
< .
5
5
3
4
Remarque : < peut s’interpréter en disant que 3 parts d’un gâteau coupé en 5 valent moins que 4 parts de ce gâteau.
5
5
Exemple :
b.
Comparaison de fractions ayant le même numérateur
Règle
Pour comparer deux fractions ayant le même numérateur, il suffit de comparer les dénominateurs : la fraction ayant
le plus grand dénominateur est la plus petite.
Exemple :
c.
4
4
> .
5
6
Comparaison à 1
Règle
Une fraction dont le numérateur est plus petit que le dénominateur est une fraction inférieure à 1.
Exemple :
d.
4
<1 ;
5
8
> 1.
7
Comparaison de fractions de dénominateurs multiples
Règle
Pour comparer deux fractions n’ayant pas le même dénominateur, on modifie l’écriture des fractions pour qu’elles
aient le même dénominateur.
2
7
Exemple : Comparer et
:
3
12
2
2×4
8
8
7
2
7
On remarque que =
=
. Comme
>
, on obtient alors que >
.
3
3×4
12
12
12
3
12
5
Division dont le diviseur est décimal
Règle
Pour effectuer une division dont le diviseur est décimal, on multiplie le numérateur et le dénominateur par 10, 100 ou
1000 . . .afin que le dénominateur soit entier.
Exemple : Pour calculer 254 ÷ 2, 31, on écrit :
254
254 × 100
25400
254 ÷ 2, 31 =
=
=
= 25400 ÷ 231.
2, 31
2, 31 × 100
231