Premiere s exercices sur la derivation 2010

Première S Exercices sur la dérivation 2010-2011
1
Exercice 1
Calculer f'(x) en précisant pour quelles valeurs le calcul est valable.
1) f(x) = 2 – x²
2 + x²
2) f(x) = 1
x²sin x.
3) f(x) = x - 4
4) f(x) = cos
2x + π
3
Exercice 2 : Déterminer une fonction polynôme
f est une fonction polynôme du second degré, C sa courbe représentative
dans un repère orthonormal (O;
→
i ;
→
j ).
Le point A de coordonnées (1;6) est un point de C, la tangente T à C au
point d'abscisse 2 est parallèle à la droite d'équation y = 10x – 5 et f(2) =
13.
Objectif : Déterminer, si elle existe, la fonction f.
1) Un polynôme est entièrement déterminé par la donnée de ses
coefficients. On pense donc à écrire f(x) = ax² + bx + c, avec a, b, c
réels (a ≠ 0).
Savoir si f existe revient à savoir si on peut trouver trois nombres a, b,
c qui répondent aux exigences de l'énoncé.
a) Pourquoi les données permettent-elles de calculer f(1) et f'(2) ?
Préciser ces valeurs.
b) Prouver que le problème posé est équivalent à : existe-t-il des
nombres a, b, c, a ≠ 0, tels que :

Première S Exercices sur la dérivation 2010-2011
2
4a + b = 10
a + b + c = 6
4a + 2b + c = 13
?
2) Vous n'avez pas l'habitude de résoudre un tel système … Mais la
première équation ne contient que deux des trois inconnues. Elle
permet alors, par exemple, d'exprimer b en fonction de a.
a) Vérifier alors que le système est équivalent à :
b = 10 – 4a
-3a + c = -4
-4a + c = -7
b) Calculer alors a et c, puis en déduire b.
c) Conclure.
Exercice 3 : Tangentes à une courbe passant par un point
Dans un repère (O;
→
i ;
→
j ), C est la courbe représentative de la fonction
f : x → x²
2 -2x + 3 et A le point de coordonnées (1;-1).
Objectif : Déterminer, si elles existent, les tangentes à C passant par A.
1) L'utilisation d'un graphique peut permettre de mieux saisir la situation.
a) A l'aide d'un traceur de courbe ou de la calculatrice, commencer par
tracer C puis placer A.
b) Le point A est-il sur C ? Conjecturer le nombre de tangentes à C
passant par A.
2) Il s'agit en fait de trouver le (ou les) point(s) N de C en lesquels la
tangente à C passe par A. Pour connaître un point de C, il suffit de

Première S Exercices sur la dérivation 2010-2011
3
connaître son abscisse. On choisit donc comme inconnue l'abscisse n de
N.
a) Trouver en fonction de n une équation de la tangente T
n
en N à C.
b) Démontrer que "T
n
passe par A" équivaut à "n² - 2n – 4 = 0".
c) Résoudre cette équation. Combien trouvez-vous de tangentes T
n
?
Concluer en plaçant les points trouvés et en traçant les tangentes.

Première S Exercices sur la dérivation 2010-2011
CORRECTION
4
Exercice b + c = 1
1) f est du type u
v avec u(x) = 2 – x² et v(x) = 2 + x²
u
v
' = u'v – uv'
v²
Or u'(x) = -2x et v'(x) = 2x
Donc f'(x) = -2x×(2 + x²) – (2 – x²)×2x
(2 + x²)² = -2x (2 + x² + 2 – x²) (2 + x²)² = -8x (2 + x²)²
f' est définie comme f sur r.
2) f = uv avec u(x) = 1
x² et v(x) = sin(x)
f' = u'v + uv'
Or u'(x) = - 2
x
3
et v'(x) = cos(x)
Donc f'(x) = - 2
x
3
sin(x) + 1
x²cos(x)
f' est définie comme f sur r
*
.
3) f(x) = u(3x – 4) avec u(x) = x
Donc f'(x) = 3
2 3x - 4
f est définie sur 
4
3 , +∞ et f' sur 
4
3 , +∞ .
4) f(x) = u
2x + π
3 avec u(x) = cos(x)
Donc f'(x) = -2 sin
2x + π
3
f et f' sont définies sur r.

Première S Exercices sur la dérivation 2010-2011
CORRECTION
5
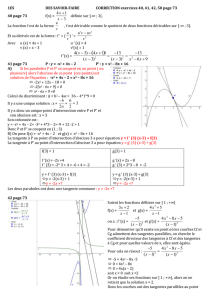
Exercice 2
1) a) Si A(1;6) ∈ C alors f(1) = 6
La tangente T à C au point d'abscisse 2 étant parallèle à la droite
d'équation y = 10x – 2, ces deux droites ont le même coefficient directeur
10 et f'(2) = 10.
b) Si f(x) = ax² + bx + c alors f'(x) = 2ax + b
f'(2) = 10
f(1)=6
f(2)=13
4a + b = 10
a + b + c = 6
4a + 2b + c = 13
2) a) En substituant b = 10 – 4a dans les deux dernières équations on
obtient le système équivalent suivant :
b = 10 – 4a
a + 10 – 4a + c = 6
4a + 20 – 8a + c = 13
b = 10 – 4a
-3a + c = -4
-4a + c = -7
b) Les deux dernières équations de ce système forme un système de
deux équations à deux inconnues a et c.
D'où : -3a + 4a = -4 + 7
Soit a = 3.
On en déduit facilement : c = -4 + 3a = -4 + 9 = 5.
Puis b = 10 – 4a = 10 – 12 = -2
c) Le polynôme est donc déterminé : f(x) = 3x² - 2x + 5