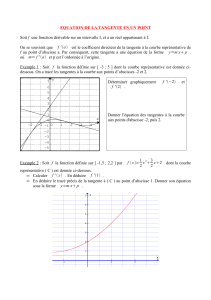
2√x 2√x √x

1 ère S DS 4 13 /12/13
Exercice 1: Pour chaque question, une seule des trois propositions est exacte. Vous indiquerez sur votre
copie le numéro de la question et vous recopierez la bonne réponse. Aucune justification n’est demandée.
Une réponse exacte rapporte 1 point ; toute réponse fausse enlève 0,5 point.
1. f est une fonction telle que pour tout nombre réel h non nul,
f ( 1+h ) −f ( 1 )
h=h2+3h−1
alors
f ' (1) est égal à ♦ 8 ♦
h2+3h−1
♦
−1
2. f est une fonction telle que
f ( 2 ) =−5
et
f ' ( 2 ) =−3
. Dans un repère, la tangente à la courbe
représentative de f au point d'abscisse 2 a pour équation :
♦
y=−3x+1
♦
y=−3x – 11
♦
y=−3x−5
3. f et g sont deux fonctions définies sur
[ 0;+∞ [
par
f
(
x
)
=
√
x
et
g ( x ) =3x – 2
alors pour tout nombre
réel
x>0
,
( f×g ) ' ( x )
est égal à :
♦
1
2
√
x+3
♦
9x−2
2
√
x
♦
6x−2
√
x
4. La fonction
f
définie sur
]
−∞;−3
2
[
∪
]
−3
2;+∞
[
par
f ( x ) =x2−1
2x+3
admet comme dérivée sur cet
intervalle la fonction définie par
♦
f ' ( x ) =2×x2+3x+1
(
2x+3
)
2
♦
f ' ( x ) =x
♦
f ' ( x ) =2x2+6x+2
4x2+9
5.
f
est une fonction dérivable sur
[ −2;3 ]
.
On a tracé ci-contre , dans un repère, la courbe représentative C de
f
et
les tangentes à C aux points d'abscisses
−1
et
0
Parmi les courbes ci-contre , quelle est celle qui
représente la fonction
f '
Pour les deux questions suivantes : le graphique ci-contre représente dans un repère, la courbe
représentative C d'une fonction f dérivable sur
[ 0;+∞ [
et deux de ses tangentes.
6. On a ♦ f ' (0) = 1 ♦ f ' (1) = 0 ♦ f ' (1) = 2
7. g est la fonction définie sur
[ 0;+∞ [
par
g
(
x
)
=1
f
(
x
)
alors :
♦ g' (0) = -3 ♦ g' (0) =
1
3
♦ g' (0) = 3

Exercice 2 : (8 points)
L'objectif de cet exercice est d'étudier la position relative de la courbe représentant une fonction
f
par rapport
à une de ses tangentes.
Partie A
Soit la fonction
g
définie sur
ℝ
par
g
(
x
)
=x3−2x2−4x+8
.
1. Étudier les variations de la fonction
g
2. Vérifier que
g
(
x
)
=
(
x−2
) (
x2−4
)
3. Étudier le signe de
g ( x )
sur
ℝ
Partie B
Soit la fonction
f
définie sur
ℝ
par
f
(
x
)
=x3−2x2+1
dont on a représenté une partie de la courbe
représentative ci-dessous :
1. Montrer que l'équation de la tangente
( T )
à la courbe
Cf
au point d'abscisse 2 est la droite d'équation
y=4x−7
2. Construire
( T )
sur le graphique.
3. Étudier la position relative de
Cf
et de
( T )
. On pourra s'aider des résultats de la partie A.
Exercice 3 : (5 point)
On veut construire une cuve métallique à partir d'une plaque carrée de 3m de côté
A chaque coin de cette plaque, on découpe un carré de
x
mètres de côté. En pliant et en soudant, on obtient
une cuve de volume
V ( x )
en m3.
1. Quelles sont les valeurs possibles de
x
.
2. Montrer que le volume de la cuve
V
(
x
)
=4x3−12 x2+9x
3. Étudier les variations de la fonction V, et en déduire la valeur de
x
qu'il faut découper afin d'obtenir
une cuve de volume maximal.

1 ère S Corrigé : DS 4
Exercice 1:
1. f est une fonction telle que pour tout nombre réel non nul h,
f ( 1+h ) −f ( 1 )
h=h2+3h−1
alors
f ' ( 1 ) =−1
2. f est une fonction telle que f (2) = -5 et f ' (2) = -3. Dans un repère, la tangente à la courbe représentative
de f au point d'abscisse 2 a pour équation
:y=−3x+1
3. f et g sont deux fonctions définies sur [0;
+∞
[ par f(x) =
√
x
et g(x) = 3x – 2 alors pour tout nombre réel x > 0
(f×g) ' (x) est égal à :
9x−2
2
√
x
4.
f
est une fonction quotient du type
u
v
, on pose
u ( x ) =x2+1
et
v ( x ) =2x+3
. D'après la formule de la dérivée du quotient on
obtient
f ' ( x ) =2x2+3x+2
( 2x+3 )
2
, en factorisant par 2 au numérateur
on obtient
f ' ( x ) =2×x2+3x+1
(
2x+3
)
2
5.
Pour les deux questions suivantes : le graphique ci-contre
représente dans un repère, la courbe représentative C d'une
fonction f dérivable sur [0;
+∞
[ et deux de ses tangentes.
a. On a ♦
f ' ( 1 ) =0
b. g est la fonction définie sur [0;
+∞
[ par g(x) =
1
f
(
x
)
alors :
♦
g' ( 0 ) =−3
Exercice 2
1. La fonction
g
est dérivable sur
ℝ
comme somme de fonctions dérivables sur
ℝ
.
On calcule
g'
(
x
)
=3x2−4x−4
.
On étudie le signe de
g' ( x )
sur
ℝ
.
g' ( x )
est un trinôme du second degré, on cherche alors ses éventuelles racines.
Δ=64
, il y a donc deux racines réelles distinctes
x1=− 2
3
et
x2=2
.
On en déduit alors le signe de
g' ( x )
sur
ℝ
sachant que
a=3
donc positif.
On dresse alors le tableau de variations de
g
à l'aide du tableau de signes de
g' ( x )
x
−∞
−2
3
2
+∞
signe de
g' ( x )
+
−
+
256
27
10
g ( x )
0
2. On développe
(
x−2
) (
x2−4
)
, on trouve alors que
(
x−2
) (
x2−4
)
=x3−2x2−4x+8
soit
g
(
x
)
=
(
x−2
) (
x2−4
)
.
3.
x2−4
est un trinôme du second degré avec deux racines évidentes,
2
et
−2
, on en déduit le signe de
x2−4
sachant que
a=1
donc positif.
On obtient le tableau de signes suivant

x
−∞
−2
2
+∞
( x−2 )
−
−
0 +
x2−4
+ 0
−
0 +
f ( x )
−
0 + 0 +
Plus malin... on remarque que
x2−4=
(
x−2
) (
x+2
)
, ainsi
g ( x ) = ( x−2 )
2
( x+2 )
donc
g ( x )
est du signe de
x+2
Partie B
1. L'équation de la tangente à la courbe au point
d'abscisse 2 est
y=f ' ( 2 )( x−2 ) +f ( 2 )
.
On calcule
f '
(
x
)
=3x2−4x
, ainsi
f ' ( 2 ) =12−8=4
.
Or
f ( 2 ) =1
, l'équation de la tangente est donc
y=4 ( x−2 ) +1
soit en développant
y=4x−7
.
2. On utilise le calcul du coefficient directeur
4=2
0,5
3. On définit la fonction
h
sur
ℝ
par
h ( x ) =4x−7
, sa courbe représentative est
donc
( T )
.
Étudier la position relative de
Cf
par rapport
à
( T )
revient donc à étudier le signe de
f ( x ) −h ( x )
.
f
(
x
)
−h
(
x
)
=x3−2x2+1−
(
4x−7
)
soit
f
(
x
)
−h
(
x
)
=x3−2x2−4x+8
, on remarque ainsi
que
f ( x ) −h ( x ) =g ( x )
.
Puisque l'on a étudié de signe de
g ( x )
dans la partie
A, on en déduit que
Cf
est au-dessus de
( T )
sur
l'intervalle
[ −2;+∞ [
Exercice 3
1. En découpant de part et d'autre du carré on remarque que
x∈
]
0; 3
2
[
2. la cuve est formée d'un carré de côté
3−2x
et la hauteur de l'arrête est
x
, ainsi le volume de la cuve
est
V ( x ) =x ( 3−2x )
2
, ainsi
V
(
x
)
=4x3−12 x2+9x
.
3. On étudie les variations de la fonction V.
V'
(
x
)
=12 x2−24 x+9
, pour simplifier les calculs on remarque que
V'
(
x
)
=3
(
4x2−8x+3
)
, on étudie
alors plus simplement le signe de
4x2−8x+3
.
Δ=16
, ainsi il y a deux racines distinctes
x1=3
2
et
x2=1
2
, on en déduit le signe de V'(x) puis les
variations de la fonction V
x0
1
2
3
2
signe de
f '
+ 0
−
0
2
f
La cuve aura un volume maximal pour
x=2
et atteindra le volume maximal de
2m3