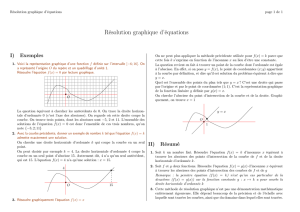
EXERCICE 1 (14 points) La courbe C d`une fonction u est donnée. 1

Lycée A.Maurois
...... Octobre CORRIGE DS N° 2 T ES3 Durée 1H20
EXERCICE 1 (14 points) La courbe Cd’une fonction uest donnée.
1. La fonction uest définie et dérivable sur Du=]−2;+∞[. Lorsque x∈Du,u(x) appartient à ] − ∞;5] d’après les indications
du graphique.
2. Sur ] −2;+∞[ l’équation u(x)=0 admet les solutions −1,5, 4,5 et 6,5 qui sont les abscisses des points de Cdont l’ordonnée
vaut 0.
3. Sur ] −2;+∞[, u(x)>0 a pour solutions les abscisses des points de Csitués au dessus de l’axe des abscisses strictement.
L’ensemble des solutions est donc J=]−1,5;4,5[∪]6,5;+∞[.
4. Pour résoudre graphiquement l’inéquation u(x)>3x−1 on trace la droite (d) d’équation y=3x−1, on repère pour quelles
valeurs de xun point d’abscisse xsur Ca une ordonnée supérieure à l’ordonnée du point d’abscisse xde (d). On ne dispose
pas de suffisamment d’informations sur ce qui se passe entre −2 et −1,5 mais on est certain que u(x)>3x−1 sur [−1,5;5].
5. On lit : u(−1) =2, u(2) =5 et u(4) =2.
6. A l’aide du graphique u0(−1) =5−2
0−(−1) =3 , u0(2) =0 ( tangente horizontale) et u0(4) =2−(−1) 4−5=−3.
7. La tangente à Cen A a pour coefficient directeur u0(4) =−3 son équation réduite est donc de la forme y=−3x+pet il faut
trouver p.
Comme A∈TA, ses coordonnées vérifient l’équation et donc 2 =−3×4+psoit p=14.
8. Tableau de variation de u: à partir de la courbe. (Remarque lim
x→−2u(x)=−∞ et lim
x→+∞u(x)=4).
9. On introduit la fonction gdéfinie par g(x)=1
xpour x∈]0;+∞[ et on note fla fonction g◦u.
a. f(x) existe ssi x∈Du=]−2;+∞[ et si u(x)∈x∈]0;+∞[. D’après la question 3. on a donc Df=J.
b. On a par définition f(x)=g(u(x)) =1
u(x)soit encore
f:x7→ u(x)7→ g(u(x)) =1
u(x).
c. Etudier les variations de fsur Df. Sur ]−1,5;2], u est croissante à valeurs dans ]0;+∞[ où gdécroît donc par composition
fdécroît sur ] −1,5;2].
Sur ]2;4,5[, u est décroissante à valeurs dans ]0;+∞[ où gdécroît donc par composition fcroît sur ]2; 4,5[.
Sur ]6,5;+∞[, u est croissante à valeurs dans ]0;+∞[ où gdécroît donc par composition fdécroît sur ]6,5; +∞[.
d. On a f(−1) =1
u(−1) =0,5f(2) =1 u(2) =0,2 et f(6) n’existe pas.
e. La formule de la dérivée d’une fonction composée g◦udes deux fonctions dérivables uet g: (g◦u)0(x)=u0(x)×g0(u(x)).
f. Calculer en utilisant ce qui précède f0(−1) =3×(−1
(−1))2=−3, f0(2) =0 et f0(6) n’existe pas.
g. Tableau des variations de f: résumé des informations précédentes.
h. Grâce au théorème fondamental de l’analyse on déduit le signe de f0(x) des variations de fsoit f0(x)>0 sur ]2;4,5[,
f0(x)<0 sur ] −1,5;2]∪]6,5;+∞[ et f0(x)=0 en 2 qui est l’abscisse d’un minimum local.
EXERCICE 2 (6 points) Soit fla fonction définie par la formule f(x)=−(4 −x)3
x2−3où xdésigne un nombre réel.
1. f(x) existe ssi x2,3 donc Df=R− {√3;−√3}.
2. Exprimer f0(x) :
Dérivée du numérateur : x7→ 3(4 −x)2
Dérivée du dénominateur : x7→ 2x,
D’où f0(x)=3(4 −x)2(x2−3) +2x(4 −x)3
(x2−3)2.
On factorise le numérateur par (4 −x)2on obtient f0(x)=(4 −x)2[3(x2−3) +2x(4 −x)]
(x2−3)2=(4 −x)2[x2+8x−9] (x2−3)2et puisque
des carrés sont positifs on obtient le résultat : f0(x) est du signe contraire de celui du trinôme −x2−8x+9.
3. On étudie le signe de x2+8x−9. Ce trinôme a deux racines −9 et 1 et il est négatif entre ses racines, d’où le signe de f0x) et
donc on en déduit les variations de f.
4. L’équation réduite de la tangente à la courbe de fau point Ad’abscisse 2 est : y=f0(2)(x−2)+f(2) =44(x−2)−8=44x−96.