son corrigé

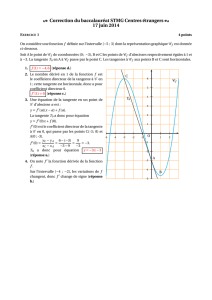
Exercice 1 :
1°) Calculons la dérivée :
2g x ax b
.
On a donc deux équations :
12g
22ab
et
24g  
44ab   
.
En faisant une soustraction des deux on obtient :
2 4 2 4a b a b      
66a
1a
.
Ce qui nous donne
0b
.
Reste à déterminer c. Pour cela écrivons l’équation de la tangente en utilisant les valeurs des coefficients trouvés :
2g x x
2
0 0 0
2y x x x x c   
(
0
x
étant le point d’abscisse 1, le point de tangence et non le point A !)
2 1 1y x c   
. Puis utilisons les coordonnées de A :
10 2 5 1 1 c   
1c
.
On a donc pour terminer :
21g x x
.
2°) Déterminons l’équation de la tangente :
Le point B nous permet d’écrire
3y mx
. Le coefficient directeur s’obtient donc en faisant les deltas de y sur x :
53 4
20
m
. L’équation de la tangente a pour équation réduite :
43yx  
.
Cette droite étant tangente à la courbe en 0, on peut donc écrire :
04h
2 0 4rs   
4s
.
En utilisant
18h
on obtient :
84rt  
4rt
. Il nous manque des données pour la résoudre, mais
qu’avons-nous oublier d’exploiter ?
Combien vaut
0h
? C’est la même valeur que celle de l’ordonnée de la tangente en 0, soit 3 !
Ce qui nous donne une nouvelle équation :
3t
. Donc
1r
, et finalement :
243h x x x  
.
3°) a) Pour déterminer l’ensemble de définition trouvons les valeurs interdites :
24 3 0xx  
, possède une racine évidente 1 (il suffit de faire la somme des coefficient) donc 3 est l’autre racine
(en utilisant le produit des racines).
Donc
\ 1,3D
.
b)
232
22
22
2
2 3 2
2
2 4 3 2 4 43
2
43 4
12
43
1
3
2
x x x x x x x
fx x
x
x x x
xx x x x
x
22
22
22
22
24
4 3 4
2
3
1x x x x
fx x x x x
.
c) Déterminons le signe de la dérivée :
210xx
24 1 4 5 0b ac      
115
2
x
et
215
2
x
.
Le signe de la dérivée est le signe de ce trinôme, donc pas besoin de faire un tableau des signes.
x
15
2
1
15
2
3
fx
- 0 +
+ 0 -
-
fx

Exercice 2 :
1°) a) Ensemble de définition de
g
: il faut que
6 5 0x
5
6
x
.
5;
6
g
D
.
Calcul de la dérivée :
63
65 2 6 5 6 5 g x x xx
.
Cette fois-ci on veut que
6 5 0x
, ce qui implique que
5;
6
g
D
.
b)
3 3 3
1 11
11
6 5 11
g  
.
2°)
311 1 11
11
yx  
3
11 1 1
11
yx
38
11 11 11 yx
.
Exercice 3 :
1°) a)
u x g x h x
2
1 1 1 1 1 1 2u x g x h x x x x x x
.
x
0 2
22xx
+ 0 - 0 +
b)
x
0 2
ux
+ 0 - 0 +
ux
20/3
16/3
2°)
2 2 2 9 9 0u g h         
.
Donc pour
;2x  
la courbe est en dessous de la droite, et
pour
2;x  
la courbe est au-dessus de la droite.
Exercice 4 :
1°)
32
f x ax bx cx d   
3 2 2
32f x ax bx cx d ax bx c
.
2°)
01f
(c’est le point D),
11f
(c’est le point A).
Calculons le coefficient directeur de
2
:
220
1f
.
Calculons le coefficient directeur de
1
:
111
1f
.
3°)
0fd
donc
1d
. De même
0fc
, donc
2c
.
Reste à déterminer a et b. Deux inconnues réclament deux équations.
1 1 2 1f a b     
2ab  
.
1 3 2 2 1f a b
3 2 3ab  
.

Multiplions la première par 2 et soustrayons.
3 2 2 2 4 3a b a b    
1a
.
Donc
12b  
3b
Ce qui nous donne :
32
3 2 1f x x x x   
2
3 6 2f x x x
4°) Les calculs sont déjà fait. Calculons les racines de la dérivée
1
.
2
3 6 2 0xx  
2
3 3 2 0xx  
9 6 3 0
133
3
x
et
233
3
x
.
x
33
3
33
3
fx
+ 0 - 0 +
fx
5°) a)
2
3
2 2 3 2 4 1 8 12 4 1 1f         
et
32
5 5 5 125 75 125 150 25 32 7
3 5 1 4 4
2 2 2 8 4 8 8 8 8 8
f     
.
b) La courbe coupe une seule fois l’axe des abscisses sur
33
;
3
, car la fonction est strictement monotone et
continue, et change de signe. Il existe donc une solution seule solution à l’équation
0fx
.
c) Voici un exemple de la procédure à suivre avec un TI :
On vise grossièrement pour commencer :
Ceci nous permet de raffiner entre 2,3 et 2,4
On affine encore entre 2,32 et 2,33 :
Ce qui nous donne l’encadrement suivant :
2,324 2,325
.
1
J’utilise les formules de réduction par moitié (b=2b’ …). Autrefois elles étaient enseignées en première S pour les élèves qui allaient un
peu plus vite que les autres, mais c’était optionnel, on peut très bien résoudre une équation du second degré sans connaître ces formules.