Exercice n°2:Echelle d`un camion de pompier On considère un

Exercice n°2:Echelle d’un camion de pompier
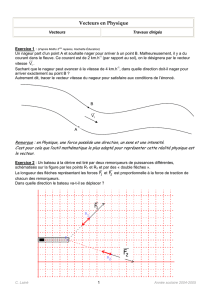
On considère un camion de pompier (1) se trouvant à l’arrêt en train de déployer sa grande
échelle. On associe au camion le repère R1111
(, , , )Bx y z
J
GJJGJG . L’échelle comporte deux parties : la
partie inférieure (2) est en liaison pivot d’axe 1
(, )Bz
J
Gavec le camion et la partie supérieure (3)
est en liaison glissière avec la partie inférieure de l’échelle. On associe à la partie inférieure de
l’échelle le repère R2221
(, , , )Bx y z
JJGJJGJG . La rotation de (2) par rapport à (1) est repérée par l’angle
. On pose BC=a (a constante positive). Le point A se trouvant à
l’extrémité de la partie supérieure de l’échelle est repéré par la distance CA=b(t) (b : fonction
du temps).
12 12
() ( , ) ( , )txx yy θ ==
JG JJGJJGJJG
Cas 1: θ(t) est quelconque
1. Déterminer le vecteur rotation )1/2(Ω
2. Déterminer le vecteur position BA
3. Calculer la vitesse de A par rapport à (1): )1/(AV .
4. A l’instant considéré, la vitesse de rotation de la partie inférieure de l’échelle est de 20
tours/min, la vitesse de sortie de la partie supérieure est de 2 m/s, a=3m et b=1m,
déterminer la norme de la vitesse du point A par rapport à (1): )1/(AV .
5. Calculer la vitesse de A par rapport à (2): )2/(AV
6. Calculer l'accélération de A par rapport à (1): )1/(Aa .
7. Vérifier l’homogénéité de votre relation.
8. Calculer l'accélération de A par rapport à (2): )2/(Aa
Cas 2: L’échelle tourne à vitesse angulaire ω constante⇒θ(t)= ω t (ω =constante=2 rad/s) et
la partie supérieure sort à vitesse constante V0 (V0=0.5 m/s)
9. Calculer la vitesse de A par rapport à (1): )1/(AV .
10. Calculer la vitesse de A par rapport à (2): )2/(AV
11. Calculer l'accélération de A par rapport à (1): )1/(Aa .
12. Calculer l'accélération de A par rapport à (2): )2/(Aa
C
a
2
x
J
JG
b(
t
)
1
x
J
G
θ
1
y
JJG
(
3
)
(
2
)
(1)

Echelle d’un camion de pompier :
Cas1 :
1)
2/1 1,2
zθ Ω=
JJJJG JJJG
2)
2
(()). BA a b t x =+
JJG JJG
3) (/1) 2 2 ..().
A
V
bx a b yθ =++
JJJJJG JJG JJG
4) A.N. : 2
2
22
(/1) 2.
.( ) 2 .(4) 8.61 /
3
A
V
bab m
π
θ
⎡⎤
⎡⎤
=+ + =+ =
⎢⎥
⎣⎦ ⎣⎦
JJJJJG 
s
5) (/2) 2
.
A
V
bx =
JJJJJG JJG
6)
2
(/1) 2 2
( ( ). ). (2. . ( ). ).
A
a b ab x b ab yθθ =−+ + ++
JJJJJG JJG JJG
θ
2
x
7)
2
:/ bms
22
().:.(/) / ab mrds msθ +=
2
.: /. / / bmsrdsmsθ =
22
().:./ / ab mrds msθ +=
8)
(/2) 2
.
A
ab =
JJJJJG JJG
Cas2 :
9) (/1) 8.01 /
A
V
ms =
JJJJJG
10) (/2) 2 0 2 ..0.5
A
/
V
bx V x m s == =
JJJJJG JJG JJG
11)
22
(/1) 0 2 2
.. ( ). 16.03 /
A
aVy abx mωω =−+=
JJJJJG JJG JJG
s
12)
(/2) 0 A
a =
JJJJJG G