COURANT ÉLECTRIQUE

Q Courant électrique – Résistance (36-101) Page 1 sur 3 JN Beury
conducteur orienté
arbitrairement
d S
d S
v
G
v
G
dvt
G
dvt
G
n
G
n
G
COURANT ÉLECTRIQUE
I. COURANT ÉLECTRIQUE
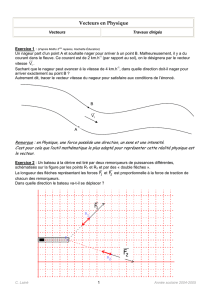
I.1 Densité volumique de courant
Le courant électrique est dû à un déplacement de charges électriques.
On considère un conducteur parcouru par un courant électrique. L’orientation est
arbitraire.
Soit un élément de surface dS. On définit n
G
le vecteur normal à dS orienté dans le même sens que le
conducteur. Le vecteur élément de surface est ddSSn=
J
JG
G
.
On définit : n la densité volumique de porteurs de charges (mobiles),
ou
mmobile
ρ
ρ la densité volumique de charges (m comme mobiles)
et q la charge d’une molécule. On a alors mnq
ρ
=
.
On considère qu’on a un seul type de porteurs de charges (des électrons par exemple).
• On appelle1 2
dqla charge qui traverse la surface d’arrivée dS
J
JG
pendant dt : elle est comprise dans le
cylindre de section dS et de longueur v dt. On a donc :
(
)
2
ddd
m
qvtS ρ
=
⋅
J
JG
G
.
On pose m
jvnqv ρ ==
GGG
le vecteur densité (volumique) de courant électrique.
Le terme volumique est sous-entendu.
• La charge dq qui traverse la surface S vaut : 2 dd dd
SS
qqjSt==⋅
∫∫ ∫∫
J
JG
G
.
L’intensité du courant électrique qui traverse S vaut : dd
dS
q
I
jS
t
=
=⋅
∫∫ JJG
G
Unité de j
G
: A.m-2.
Le sens du courant est le sens dans lequel se déplaceraient des charges positives.
a) Cas particulier
Si j
G est uniforme. On a
I
jS= avec S surface perpendiculaire aux lignes de courant. On emploie
le terme « surface d’arrivée ».
b) Généralisation avec plusieurs types de portes de charges
On rencontre souvent des exercices avec plusieurs types de porteurs de charges : plasma par exemple
constitué de cations et d’anions. L’indice 1 désigne par exemple le cation et 2 l’anion.
Le vecteur densité (volumique) de courant est : ii i ii
i
j v nqv ρ ==
∑
G
G
G
i
ρ
est la densité volumique de charges de type i en C.m-3.
• Dans le cas du plasma, i varie de 1 à 2. Les deux types d’ions se déplacent en sens inverse ; ils
donnent alors des contributions de même sens à la densité volumique de courant car 1
ρ
et 2
ρ
sont
de signes contraires.
• Dans un métal, lors porteurs de charge sont les ions du réseau cristallin et les électrons de
conduction. La densité volumique de courant est el el
jv ρ =
G
G
dans un référentiel lié au métal où les
ions sont fixes.
1 La notation d2q rappelle qu’il y a deux infiniment petits : dS et dt.

Q Courant électrique – Résistance (36-101) Page 2 sur 3 JN Beury
d l
σ
v t d
A
B
n
G
v
G
S
j
G
S
j
G
d z
L
S
j
G
conducteur orienté
arbitrairement
L
S
j
G
I.2 Densité surfacique de courant
Dans certains exercices, les charges se déplacent sur une très faible épaisseur. On peut considérer alors qu’on
a des courants en surface (voir cours sur les équations de Maxwell et relations de passage). On appelle
σ
la
densité surfacique de porteurs de charges mobiles.
Soit un élément de longueur dl. On définit n
G
le vecteur normal à dl orienté dans le même sens que le
conducteur.
• On appelle d2q la charge qui traverse la « ligne d’arrivée » dl. On a alors
()
2
dddqvtln σ =⋅
GG
. On pose
On pose s
jv
σ
=
GG le vecteur densité surfacique de courant électrique.
On en déduit 2 ddd
s
qjlnt=⋅
GG.
• On appelle dq la charge qui traverse la « ligne d’arrivée » AB. Il faut faire la somme des contributions
précédentes.
L’intensité du courant électrique vaut: dd
d
B
S
A
q
I
jln
t
== ⋅
∫
G
G
a) Cas particulier
Si S j
G est uniforme : S
I
jL= avec L « ligne d’arrivée » perpendiculaire aux lignes de courant.
Dans les exercices, on aura très souvent un cylindre parcouru
par des courants surfaciques.
On a alors : 2
S
I
jR
π
= avec R le rayon du cylindre.
b) Relation entre le vecteur densité surfacique de courant et le vecteur densité volumique de courant
La méthode est la même qu’avec les charges. Il faut calculer l’intensité de deux façons :
Courant surfacique : S
I
jL
=
Courant volumique : d
I
jzL
=
On en déduit : d
S
jjz=

Q Courant électrique – Résistance (36-101) Page 3 sur 3 JN Beury
d z
L
dl
JJG
1
I
2
I
3
I
1
j
G
2
j
G
3
j
G
2
I
1
I
3
I
1
S
2
S
3
S
II. VECTEUR ÉLÉMENT DE COURANT
Dans de très nombreuses relations : loi de Biot et Savart 0
2
d^
d4
KM
Il u
BKM
µ
π
→
=
J
JG
G
G
, force de Laplace
()
dd^
F
Il B=
JJJGJJGG
, on définit le vecteur élément de courant : ddCIl=
J
JJGJJG
On a :
() ()()
ddddddd
S
I
l jLz l j jz Ll j S τ === =
.
L’élément de courant est : ddd d
S
CIl j jS τ == =
J
JJGJJG
G
G
a) Confusions fréquentes
Il ne faut pas confondre les longueurs, surfaces et volumes définis précédemment.
ddd d
S
CIl j jS τ == =
JJJGJJGGG
: dl
J
JG
désigne le vecteur longueur de déplacement du courant, dS est la surface de
déplacement du courant et d
τ
désigne le volume de déplacement du courant.
On utilise souvent les expressions simplifiées : I = j S et I = jS L.
S est la « surface d’arrivée » perpendiculaire aux lignes de courant.
L est la longueur de la « ligne d’arrivée » (penser aux cyclistes…) perpendiculaire aux lignes de courant.
III. CAS DU RÉGIME STATIONNAIRE
En régime stationnaire (on dit aussi permanent), la densité volumique de charge et la densité volumique de
courant ne dépendent pas du temps. On admet les propriétés suivantes (voir démo cours de Spé) :
En régime permanent,
• j
G
est à flux conservatif
• Pour toute surface fermée, d0
ext
S
jS⋅=
∫∫ JJG
G
w
• Un tube de champ transporte un flux constant.
On peut donc définir l’intensité d’un fil : c’est l’intensité qui traverse une section quelconque S de ce fil qui
matérialise un tube de courant. Le choix de l’orientation de S correspond au choix d’un sens positif pour I le
long du fil.
Démonstration de la loi des nœuds en régime permanent.
¾ Méthode 1 : j
G
est à flux conservatif.
Soit S la surface fermée définie par S1, S2, S.3 et Slat :
12 3
123
12 3
d0 d d d 0
ext ext ext ext
SSSS
jS jS j S jS⋅==⋅+⋅ +⋅+
∫∫ ∫∫ ∫∫ ∫∫
JJG JJG JJG JJG
GGGG
w
Or
11
11
11 1
dd
ext
SS
I
jS jS=⋅=−⋅
∫∫ ∫∫
JJG JJG
GG
d’après l’orientation du conducteur :
On a donc : 123
d0
ext
S
jS I I I⋅==−++
∫∫ JJG
G
w
¾ Méthode 2 : On peut utiliser le raisonnement utilisé dans le cours de thermodynamique pour les
systèmes ouverts à plusieurs entrées et plusieurs sorties.
Le système ouvert (partie commune PC) est constitué de S1, S2, S.3 et Slat. Soient dq1 la charge qui rentre
pendant dt à travers la surface S1, dq2 la charge qui sort pendant dt à travers S2 et dq3 la charge qui sort
pendant dt à travers S3.
En régime permanent, on a : 123
ddd 0qqq−+ + =, d’où : 123 0III
−
++=.
On raisonne sur la charge au lieu de raisonner sur la masse.