le magnétisme observations et lois expérimentales

Q Le magnétisme – observations expérimentales (36-102) Page 1 sur 5 JN Beury
O
z
u
G
B
G
M
G
θ
Sud
Nord
M
G
Sud Nord
M
G
B
G
LE MAGNÉTISME
OBSERVATIONS ET LOIS EXPÉRIMENTALES
I. ACTIONS MAGNÉTIQUES SUBIES PAR UN AIMANT
I.1 Action d’un aimant sur un aimant
Les aimants exercent entre eux des forces magnétiques. On parle alors de magnétisme.
Deux pôles d’un aimant de même nature se repoussent : un pôle Nord et un pôle Nord se repoussent, un pôle Sud et
pôle Sud se repoussent.
Deux pôles de nature différente s’attirent : un pôle Nord et un pôle Sud s’attirent.
Une boussole est un petit aimant allongé libre de ses rotations qui s’oriente dans une direction donnée.
On a donc un moyen de caractériser la direction et l’intensité des actions magnétiques exercées par une distribution D
d’aimants. On peut ainsi définir le champ magnétostatique
(
)
BM
G
.
La direction et le sens de la boussole définissent donc la direction et le sens du champ magnétostatique. On va voir que
la période des petites oscillations peut définir la valeur du champ.
La boussole est équivalente à un aimant de moment magnétique
M
G
, vecteur caractéristique de
l’aimantation.
Si on place la boussole dans un champ magnétique extérieur B
G
, elle s’oriente dans la même direction et le même
sens que le champ magnétostatique.
Expérimentalement, on peut montrer que le moment du couple subi par un aimant placé dans un champ
magnétostatique vaut : ^
M
BΓ=
G
G
G.
C’est une expression formellement identique à ^pEΓ=
G
G
G
: moment subi par un dipôle placé dans un champ
électrostatique.
Exercice : équation différentielle au voisinage de la position d’équilibre 0
θ
=
.
On applique le théorème du moment cinétique pour un solide en rotation autour d’un axe fixe. On note
J
le moment
d’inertie de l’aimant. Dans un référentiel galiléen, on a :
2
2
dd sin
ddz
JJ MB
tt
ωθ
θ
==Γ=− . On en déduit :
2
2
dsin 0
d
MB
tJ
θθ
+
=.
Dans le cas de petites oscillations autour de la position d’équilibre 0
θ
=
, on peut effectuer un développement limité
de sin
θ
au premier ordre. On a alors :
2
2
d0
d
MB
tJ
θθ
+
=. C’est l’équation d’un oscillateur harmonique.
On pose : 2
0
M
B
J
ω =. La période propre est 0
0
22
J
T
M
B
ππ
ω
== .

Q Le magnétisme – observations expérimentales (36-102) Page 2 sur 5 JN Beury
I.2 Action d’un courant sur un aimant
En 1820, Oersted observe par hasard qu’une boussole est déviée quand on l’approche d’un fil métallique parcouru par
un courant.
http://fr.video.yahoo.com/watch/616770/2930997
http://brunelleschi.imss.fi.it/museum/esim.asp?c=500181
On considère un fil perpendiculaire au plan quadrillé parcouru par un courant orienté vers le haut.
Pour établir la carte de champ, on peut disposer un grand nombre de petites boussoles dans le plan quadrillé.
On observe que le champ est orthoradial. Les lignes de champ sont des cercles ayant le fil pour axe.
On peut montrer expérimentalement que le champ magnétostatique s’écrit en coordonnées cylindriques :
0
2
I
Bu
r
θ
µ
π
=
GG avec 71
0410H.m
µπ
−−
=× = perméabilité du vide. Le champ B
G
vérifie la règle de la main droite.
II. ACTIONS MAGNÉTIQUES SUBIES PAR UN TRONÇON DE CIRCUIT
II.1 Action d’un aimant sur un tronçon de circuit
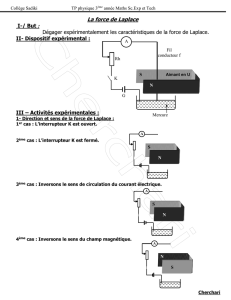
Expérience du rail de Laplace :
http://sciencesappliquees.free.fr/flash/raillaplace.html
Le champ magnétique est dirigé du Nord vers le Sud : en effet, la face Nord de la boussole est attirée par la face
Sud de l’aimant.
N
S

Q Le magnétisme – observations expérimentales (36-102) Page 3 sur 5 JN Beury
I
B
G
dl
J
JG
d
F
G
À t = 0, la barre est immobile. On constante que la barre métallique, pouvant rouler sur des rails, est déplacée vers la
droite. Elle est parcourue par un courant I qui vient vers nous, plongée dans un champ magnétostatique dirigé vers le
bas. On peut montrer expérimentalement qu’elle subit la force de Laplace dirigée vers la droite : dd^
F
Il B=JJG
GG
Soit un fil conducteur parcouru par un courant I placé dans un champ magnétique B
G. Le conducteur est
orienté arbitrairement (comme tout circuit électrique). Le vecteur longueur de déplacement du courant dl
J
JG est
nécessairement orienté dans le même sens (voir chapitre sur le courant électrique).
La force exercée par le champ magnétique sur ce conducteur est appelée force de Laplace. Elle vaut :
dd^
F
Il B=
J
JG
G
G
Remarque : dl
JJG représente le déplacement du courant par rapport au conducteur.
II.2 Action d’un circuit sur un tronçon de circuit
a) Expérience d’Ampère
On considère deux fils longs parallèles distants de D.
Si les courants I1 et I2 sont dans le même sens, on constante qu’il existe une force attractive entre les deux fils.
b) Interprétation
Les deux fils sont parallèles à Oz et distants de 12 x
A
ADu=
J
JJJG
G
Le champ magnétique créé par le fil 1 au niveau du fil 2 est : 01
12
y
I
Bu
D
µ
π
=
G
G
(voir calcul dans le chapitre sur les
calculs de champ magnétostatique). La force subie par un élément de longueur 22
dd
x
llu=
J
JG G du fil 2 est donc :
012 2
12 2 2 1
d
dd^2x
I
Il
F
Il B u
D
µ
π
→
−
==
JJG
GG G. Une longueur L du fil 2 subit la force : 012
12 2 2 1
d^ 2x
I
IL
F
Il B u
D
µ
π
→
−
==
J
JG
G
GG
La force est proportionnelle au produit I1I2. Elle est attractive si les courants sont dans le même sens, répulsive s’ils
sont en sens inverse.
c) Définition légale de l’ampère
La définition légale de l’ampère est basée sur l’interaction entre deux fils conducteurs infinis et parallèles.
L’ampère est l’intensité d’un courant constant qui, maintenu dans deux conducteurs rectilignes, infinis,
parallèles, de sections circulaires négligeables et distants de 1 m produit une force d’interaction entre ces
deux conducteurs égale à 2×10-7 N par mètre de conducteurs.
Cette définition fixe en même temps la constante 0
µ
(perméabilité du vide) à la valeur 4
π
×10-7 H.m-1.
III. ACTIONS MAGNÉTIQUES SUBIES PAR UN FAISCEAU DE PARTICULES
Expérience de Thomson (1890) : un faisceau d’électrons émis par une cathode et se déplaçant à l’intérieur d’un ampoule de
verre vidée d’air en présence d’un champ magnétostatique.
Soit une charge q, de vitesse v
G et plongée dans un champ magnétique B
G
.
Elle subit la force magnétique : ^
F
qv B=
G
G
G qui est un cas particulier de la force de Lorentz :
^
F
qE qv B=+
G
GG
G

Q Le magnétisme – observations expérimentales (36-102) Page 4 sur 5 JN Beury
I
A
B
H
I
B
G
dl
J
JG
d
F
G
B
G
L
F
G
IV. NE PAS CONFONDRE LA FORCE DE LAPLACE ET LA FORCE DE LORENTZ
Soit un fil conducteur parcouru par un courant I placé dans un champ magnétique B
G
. Le conducteur est orienté
arbitrairement (comme tout circuit électrique). Le vecteur longueur de déplacement du courant dl
J
JG est
nécessairement orienté dans le même sens (voir chapitre sur le courant électrique).
La force exercée par le champ magnétique sur ce conducteur est appelée force de Laplace. Elle vaut :
dd^
F
Il B=
J
JG
G
G
Remarque : dl
JJG représente le déplacement du courant par rapport au conducteur.
Si on a des courants surfaciques, la force de Laplace est : dd^
S
F
jSB=
G
G
G
.
Si on a des courants volumiques, la force de Laplace est : dd^
F
jB τ =
G
G
G
.
http://sciencesappliquees.free.fr/flash/raillaplace.html
La justification sera étudiée dans le chapitre sur l’effet Hall. On peut demander de vérifier que la somme des forces de
Lorentz est égale à la force de Laplace, car c’est le champ de Hall qui transmet les forces de Lorentz au réseau.
Attention aux confusions :
¾ La force de Laplace s’applique sur un CONDUCTEUR parcouru par un courant I : dd^
F
Il B=JJG
GG
¾ La force de Lorentz s’applique sur une particule chargée q : ^
F
qE qv B=+
G
GG
G
L’action mécanique de Laplace s’exerçant sur un circuit filiforme fermé de contour
Γ
a pour résultante : d^
L
F
IlB
Γ
=∫
J
JG
GG
v
et
a pour moment résultat en un point A quelconque :
(
)
^d^
A
I
AM l B
Γ
Γ=∫
J
JJJGJJG
G
G
v
.
Cas particulier très fréquence d’un segment AB parcouru par un courant I placé dans un champ extérieur
uniforme. La force subie par ce segment est ^
L
F
IAB B=
J
JJG
G
G. La résultante des forces de Laplace est équivalente à une
force unique appliquée au milieu H de [AB].
En effet,
()
d^ d ^ ^
BB
LAA
F
IlBI lBIABB== =
∫∫
JJGJJGJJJG
GG GG
. Le champ magnétique étant uniforme, ces forces sont réparties
uniformément sur AB. Il est facile de vérifier que le moment des forces de Laplace sur AB est nul en H.

Q Le magnétisme – observations expérimentales (36-102) Page 5 sur 5 JN Beury
Remarques :
¾ Nous verrons que la densité
volumique de charge dans un métal
est nulle en régime permanent et en
régime variable de fréquence
inférieure à 1014 Hz (domaine de
validité de la loi d’Ohm). Dans ces
conditions, le champ électrique est
sans action sur la conduction.
¾ L’action de Laplace exercée par un
champ magnétique sur un circuit peut
être considérée aussi comme l’action
exercée par les courants qui sont à la
source de ce champ magnétique. Le
circuit créé lui-même un champ
magnétique et exerce sur ces courants
une action mécanique. Dans le cadre
de l’ARQS, cette action est égale et
opposée à celle qu’il subit en vertu du
théorème des actions réciproques.