Le Cours

Cours 1
ère
ST2S ©E. Poulin Page 1
Activité 1 p 6
Activité 2 p 7
1.1. Proportion (ou fréquence)
1. Pourcentage exprimant une Proportion
Soit E un ensemble ayant n
A
éléments et A une partie de E ayant n
E
éléments
La proportion ou fréquence d’une sous-population A dans une population E est le rapport des
effectifs :
E
A
n
n
p== E de déléments Nombre A de élémentsd' Nombre
Dire que A représente x% de E équivaut à :
100
x
n
n
E
A
= . On note la fréquence
( )
E
A
E
n
n
Af =
Exemple :
Dans un service d’hôpital de 28 lits, 21 sont occupés.
Proportion de lits occupés ? réponse :
4
3
28
21 =
En pourcentage ? réponse
100
75
75,0
4
3== .
Il y a donc 75% des lits qui sont occupés.
 Attention aux écritures. On n’écrit pas %7575,0
=
ou %75
100
75 =
Quel que soit le choix de l’écriture, une proportion est toujours un nombre compris entre 0 et 1.
2. Addition de pourcentage, Pourcentage de pourcentage
Si C représente y% de B et si B représente x% de E, alors C représente
100
yx
×
% de E
Exemple : Dans une maison de retraite 88% des personnes ont plus de 78 ans dont 65% sont des
femmes. Quelle est la part des femmes de plus de 78 ans dans la maison de retraite ?
Addition de pourcentage :
On ne peut additionner des proportions que dans le cas de deux ensembles DISJOINTS A et B.
Exemple : Dans une association de quartier chaque adhérent pratique un seul sport. 26% des
adhérents pratique le judo, 35% la boxe, 12% la musculation, le reste la gymnastique.
Combien pratique un sport de combat ? 35% + 26% = 61%.
Exercices : p28 1 – 2 – 3 – 5 – 7 – 8 – 13 – 24 - 14 – 16 – 18 – 22 – 25 – 28 – 30 – 31.
10 – 11 – 17 – 19 - 20
Tableur sur papier 6
TABLEUR :
• Fichiers TP00-TP01-TP02-TP03-TP04
1
1. . P Po ou ur rc ce en nt ta ag ge e, , f fr ré éq qu ue en nc ce e. .

Cours 1
ère
ST2S ©E. Poulin Page 2
On se place dans un repère
(
)
jiO
r
r
,; orthonormé ou orthogonal.
2.1. Coefficient directeur
On considère une droite
∆
, non parallèle à l’axe des ordonnées, A et B deux points distincts de
cette droite.
Le coefficient directeur de la droite est
AB
AB
xx yy
m−
−
= .
Cas particulier utilisé pour tracer une droite : si 1+=
AB
xx , alors
AB
yym −= . Ainsi,
myy
AB
+=
Si 0
>
m , la droite « monte ». Si 0
=
m la droite est « horizontale Si 0
<
m , la droite « descend ».
•
Deux droites sont parallèles si elles ont même coefficient directeur
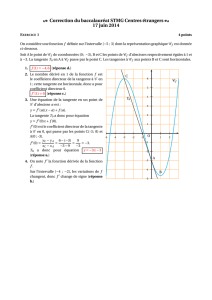
1) Comment déterminer le coefficient directeur d’une droite donnée graphiquement ?
Méthode 1 : On repère deux points A et B de la droite, puis on calcule le coefficient directeur
avec l’égalité
AB
AB
xx yy
m−
−
= .
Méthode 2 : On se place sur la droite. On se décale d’une unité vers la droite et on « descend »
ou on « monte » pour rejoindre la droite. La distance ainsi parcourue donne la valeur du
coefficient directeur, positif si on est monté, négatif si on est descendu.
Exemple
2) Comment tracer une droite dont on connaît un point et le coefficient directeur ?
• On place le point connu. A partir de ce point, on se « déplace » de 1 vers la droite
parallèlement à l’axe des abscisses.
• Si le coefficient directeur est positif, on monte de sa valeur parallèlement à l’axe des
ordonnées et on marque le point.
Si le coefficient directeur est négatif, on descend de sa valeur absolue parallèlement à
l’axe des ordonnées et on marque le point.
•
On trace alors la droite passant par le point de départ et ce point.
2
2. . D Dr ro oi it te es s – – F Fo on nc ct ti io on n a af ff fi in ne e
i
r
j
r
x
y
i
r
j
r
x
y
i
r
j
r
x
y
m
1
1
m
A
B
A
A
B
B

Cours 1
ère
ST2S ©E. Poulin Page 3
Exemple
2.2. Equation de droite
Toute droite
∆
non parallèle à l’axe des ordonnées admet une équation de la forme
p
mx
y
+
=
,
où m et p sont des réels.
Le nombre m est le coefficient directeur de la droite
Le nombre p est appelé l’ordonnée à l’origine de la droite (ordonnée au point d’abscisse 0)
Dans le cas où
∆
est parallèle à l’axe des ordonnées, tous les points de la droite ont même
abscisse. Si on note k cette abscisse, la droite
∆
a pour équation kx
=
1) Comment déterminer l’équation réduite d’une droite non parallèle à l’axe des
abscisses, définie par deux de ces points ?
1. On calcule le coefficient directeur
AB
AB
xx yy
m−
−
=
2. On écrit que les coordonnées du point A vérifient l’équation réduite pmxy
AA
+= , puis
on calcule p .
3. On écrit l’équation.
Exemple
2) Comment tracer une droite dont on connaît l’équation réduite y = mx + p ?
• On place l’ordonnée à l’origine de coordonnées
(
)
p;0
• A partir de ce point, on se déplace d’une unité vers la droite parallèlement à l’axe des
abscisses puis on monte ( si )0
>
m ou on descend (si 0
<
m ) de la valeur absolue du
coefficient directeur parallèlement à l’axe des ordonnées. On marque ce point.
• On trace alors la droite passant par les deux point placés.
Exemple
2.3. Fonction affine
Soit la fonction f définie par :
x ax b
IR IR
a+
→
où a et b sont des nombres réels donnés,
indépendants de x , et où a n’est pas nul : f est une fonction affine
La représentation graphique d’une fonction affine est une droite. Dans le cas d’une fonction
linéaire ( b =0), la droite passe par l’origine du repère
Variations – Tableau de variations
Cas a>0
f est strictement croissante sur IR Cas a<0 f est strictement décroissante sur IR
x
−∞
+∞
x
−∞
+∞
(
)
xf
+∞
−∞
(
)
xf
+∞
−∞

Cours 1
ère
ST2S ©E. Poulin Page 4
Cas Particulier : La fonction identité (
x
x
a
)
C’est une droite
passant par l’origine du repère,
de coefficient directeur 1.
Exercice 37 à 44 page 72
Signe de ax + b
x
−∞
a
b
−
+∞
Signe de
ax+b
Signe de (- a ) 0 Signe de ( a )
2.4. Utilisation de la calculatrice
• Puissance
• Tableau de valeurs
• Graphique
a>0 a<0
-5
-4
-3
-2
-1
0
1
2
3
4
5
-5 -4 -3 -2 -1 0 1 2 3 4 5

Cours 1
ère
ST2S ©E. Poulin Page 5
Activité 1 p 102
Activité 2 p 104
3.1. Introduction - Vocabulaire
A l’origine (en Chine 2000 ans avant JC, en égypte 1700 ans avant JC, puis dans l’empire
romain), la statistique (du latin « Status » : Etat) rassemblait des informations intéressant l’état,
concernant la P OPULATION , dont les éléments sont des I NDIVIDUS et consiste à observer, étudier
un même aspect de chaque individu appelé V ARIABLE OU C ARACTERE .
On distingue deux types de caractères :
• Les caractères Q UALITATIFS (profession, couleur des yeux...).
• Les caractères Q UANTITATIFS que l’on peut mesurer. Ces valeurs peuvent être
regroupées en C LASSES (
[
[
[
[
1 201 50 1 501 60 m m m m ; , ; ...)
L’ E FFECTIF n d’une valeur de la variable est le nombre d’individus correspondant à une
même valeur.
La F REQUENCE d’une valeur est le quotient de l’effectif de cette valeur par l’effectif total
de la population.
n
n
f
i
i
=
Remarque : Les fréquences sont des nombres compris entre 0 et 1, dont la somme est 1. Elles sont souvent
exprimées en pourcentage ou transformée en degré pour la construction d’un diagramme circulaire.
3.2. Représentations graphiques
1. Diagramme en bâtons, diagramme circulaire
Temps quotidien passé devant la télévision Pourcentage des télespectateurs
moins de 1 h 10,1%
[1 h ; 2 h[ 15,1%
[2 h ; 3 h[ 17,1%
[3 h ; 4 h[ 16%
[4 h ; 8 h[ 41,7%
Diagramme en bâtons
0%
10%
20%
30%
40%
50%
Diagramme circulaire
moins de 1
h
[1 h ; 2 h[
[2 h ; 3 h[
[3 h ; 4 h[
[4 h ; 8 h[
Ce type de diagramme est privilégié
dans le cas d’un caractère discret Les angles et donc les aires des secteurs sont proportionnels aux
effectifs
3
3. . S St ta at ti is st ti iq qu ue e
Exemple :