1°S2013 Activité tangente et nombre dérivé

Activité n°1 :
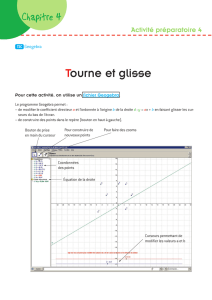
1. Démarrer le logiciel GeoGebra.
a) Tracer la courbe représentative C de la fonction f définie sur ℝ par
f
x
=
2
x
2
−
x
2
en entrant dans la
barre de saisie :
b) Créer un curseur a allant de -5 à 5 avec un pas de 1, puis un curseur h allant de 0 à 1 avec un pas de
0,01.
c) Construire les points A et M de coordonnées respectives (a ; f (a)) et (a + h ; f (a + h)) en saisissant :
et puis tracer la droite (AM) et faire apparaître sa pente (dans le menu ).
d) Déterminer une formule permettant d'obtenir le coefficient directeur de la droite (AM) en fonction de a et
de h.
e) Prendre la valeur a = -1.
Partir de h = 1 et faire diminuer la valeur du curseur h en utilisant la flèche gauche pour aller de 1 à 0,01.
Observer la valeur de la pente. Vers quelle valeur « limite » semble-t-elle se rapprocher ?
b) Que se passe-t-il lorsque h = 0 ?
c) On souhaite « tracer la droite (AM) » même lorsque h = 0. Pour cela on va tracer la droite passant par A et
dont le coefficient directeur est la valeur « limite » de la pente.
Calculer l'équation réduite de cette droite (c'est-à-dire sous la forme y =mx + p).
d) Construire la droite en saisissant son équation réduite dans la barre de saisie.
Cette droite est appelée tangente à la courbe C au point A d'abscisse -1 et son coefficient directeur est
noté f '(-1)
e) A l'aide du logiciel, conjecturer f '(1) et déterminer l'équation de la tangente à C au point d'abscisse 1.
Construire cette droite.
3. En modifiant la valeur du curseur a, compléter le tableau suivant :
a-3 0 2 5
f '(a)

Activité n°2 :
On donne le programme suivant : NbDeriv
Ce programme permet d'entrer une fonction f ainsi qu'un nombre a , puis d'obtenir un tableau où l'on peut
observer les valeurs de
f
a
h
−
f
a
h
pour des valeurs de h se rapprochant de 0.
1. a) Écrire ce programme dans la calculatrice.
La fonction DelVar se trouvent de la manière suivante :
Les fonctions list1, list2 … se trouvent de la manière suivante :
b) Tester ce programme pour la fonction f définie sur ℝ par
f
x
=
2
x
2
−
x
2
, a = -1 et N = 100.
Quelle semble être la valeur « limite » vers laquelle se rapproche la quantité
f
a
h
−
f
a
h
?
Cela correspond-il à la valeur trouvée dans l'activité n°1 ?
c) Vérifier les autres valeurs trouvées dans l'activité n°1 en modifiant la valeur de a.
2. Soit f la fonction définie sur ℝ par
f
x
=
5
x
3
−
2
x
2
3
x
1
. Compléter le tableau suivant à l'aide du
programme (on complétera en faisant des conjectures) :
a-3 0 2 5
f '(a)
3. Soit f la fonction définie sur ]–∞ ; 0[ ∪ ]0 ; +∞[ par fx=
1
x. Compléter le tableau suivant à l'aide du
programme (on complétera en faisant des conjectures) :
a-2 -1 -0,5 0,25 1 2
f '(a)