5.3 L`aire de la surface d`un prisme But de leçon - Ms M

5.3L’airedelasurfaced’unprisme
But de leçon :
- Établir la relation entre les figures a deux dimensions et trois dimensions
- Trouverlaformulepourl’aired’unprismedroit
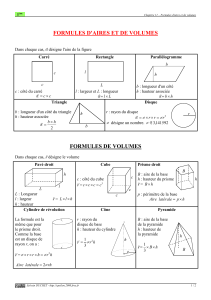
dessus/dessous face coté
Dessinez un développement de ce prisme rectangulaire :
Quel type de figure est chaque des faces? _________________________
Comment trouve-t-onl’airede cette figure?
Enutilisantledéveloppement,onvatrouverl’airedelasurfacetotale
Aire de la surface (l’aire totale) : nombre des unités carrées nécessaires pour couvrir un objet.
C’estaussila somme des aires detoutesdesfacesd’unobjet
Alorsl’aireduprismerectangulairedansl’exemple ci-dessus :
1) Quelestl’airedelafacededessus?
2) Quelestl’airede la face?
3) Quelestl’airedelafacedecôté?
4) Quel est l`aire total du prisme?

Ex. Trouvez l`aire totale d`un prisme avec les côtés de 16, 8 et 3
Comment trouve-t-onl’aired’unprisme triangulaire?
Le prisme a _____faces triangulaires et ____ faces rectangulaires
L`aire d`un triangle est :
Note : un triangle équilatéral est un triangle avec 3 côtés égaux et 3 angles égaux
Un triangle isocèle est un triangle avec 2 côtés égaux
Ex. Calculez l`aire de ce prisme triangulaire
Devoir : p. 180 #3,5,6,7,8,10, 12, 16*