3.25

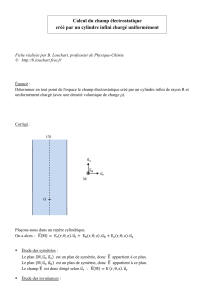
25. a) Le schéma ci-dessous présente une coupe transversale, ou mieux, une coupe en bout, du cylindre chargé (un
cercle plein). Supposons une surface de Gauss sous la forme d’un cylindre de rayon ret de longueur coaxiale
avec le même axe que le cylindre chargé. La coupe en bout de la surface de Gauss est indiquée en pointillé.
La charge intérieure qu’elle renferme est q ρ V  π r2 ρ , où V π r2est le volume du cylindre.
Si
ρ est positive, les lignes de champ électrique s’orientent radialement vers l’extérieur. Elles sont normales par
rapport à la surface de Gauss et distribuées uniformément sur sa longueur. Par conséquent, le flux net qui circule
dans le cylindre de Gauss est ΦEAcylindre E(2 π r). À présent, en appliquant le théorème de Gauss, on obtient
2πε0rE =πr2ρ =⇒E=ρr
2ε0
.
b) Ensuite, on considère une surface de Gauss cylindrique dont le rayon rR. La charge intérieure est la charge
nette contenue dans une section du cylindre chargé de longueur l. Cela signifie que q
π R2 ρ . Dans ce cas,
le théorème de Gauss permet d’écrire
2πε0rEext =πR2ρ =⇒Eext =R2ρ
2ε0r.