Exercice 1 : Déterminer le périmètre et l`aire du secteur hachuré

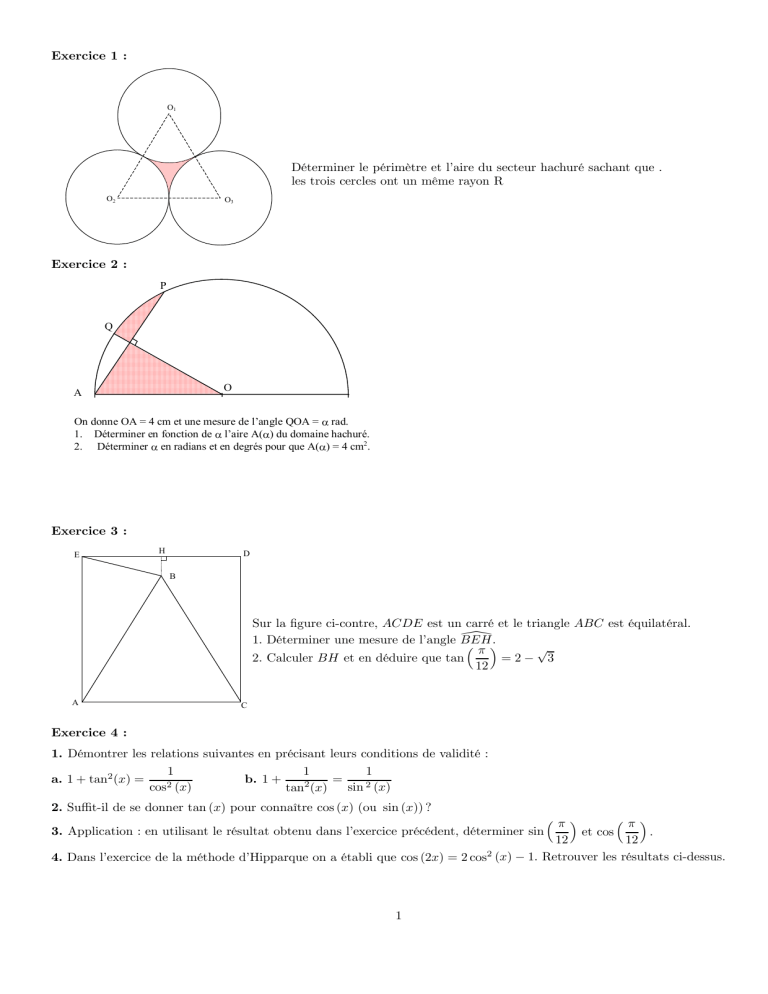
Exercice 1 :
O1
Déterminer le périmètre et l’aire du secteur hachuré sachant que .
les trois cercles ont un même rayon R
O2
O3
Exercice 2 :
P
Q
Q
O
A
On donne OA = 4 cm et une mesure de l’angle QOA = α rad.
1. Déterminer en fonction de α l’aire A(α) du domaine hachuré.
2. Déterminer α en radians et en degrés pour que A(α) = 4 cm2.
Exercice 3 :
E
H
D
B
Sur la figure ci-contre, ACDE est un carré et le triangle ABC est équilatéral.
\
1. Déterminer une mesure de l’angle BEH.
³π´
√
2. Calculer BH et en déduire que tan
=2− 3
12
A
C
Exercice 4 :
1. Démontrer les relations suivantes en précisant leurs conditions de validité :
a. 1 + tan2 (x) =
1
cos2 (x)
b. 1 +
1
1
=
sin 2 (x)
tan2 (x)
2. Suffit-il de se donner tan (x) pour connaître cos (x) (ou sin (x)) ?
³π´
³π´
et cos
.
12
12
4. Dans l’exercice de la méthode d’Hipparque on a établi que cos (2x) = 2 cos2 (x) − 1. Retrouver les résultats ci-dessus.
3. Application : en utilisant le résultat obtenu dans l’exercice précédent, déterminer sin
1
Exercice 1 :
π
\
\
1. O1 O2 = O2 O3 = O1 O3 = 2R. Le traingle O1 O2 O3 est donc équilatéral et O\
.
1 O2 O3 = O2 O3 O1 = O3 O1 O2 =
3
π
Ils interceptent donc sur chaque cercle un arc dont la longueur est R.
3
La longueur totale du secteur hachuré est donc de πR.
π
2. L’aire recherchée est s’obtient en retranchant l’aire des trois secteurs angulaires (d’angle au centre ) à l’aire du triangle
3
équilatéral O1 O2 O3 .
√
3
La base du triangle mesurant 2R, sa hauteur mesurera 2R ×
(Pythagore ou trigo) et son aire
2
Ã
Ã
√ !
√ !
√
1
1
3
3
A1 = 2R × 2R ×
× ⇒ A1 = 2R × 2R ×
× = R2 3
2
2
2
2
L’aire d’un secteur angulaire intercepté par un angle x se calcule par proportionnalité :
Angle (en radians)
Aire (en unité d’aire)
Ici, pour x =
2π
πR2
πR2 × x
R2 × x
x
avec A(x) =
⇒ A(x) =
A(x)
2π
2
³√
√
π
R2 × π
R2 × π
π´
3−
on obtient A2 =
. L’aire recherchée vaut donc A = A1 −3A2 = R2 3−3×
⇒ A = R2
3
6
6
2
Exercice 2 :
1. Un propriété bien connue du cercle : la droite (OQ) , perpendiculaire à la corde [AP ] passe son milieu (c’est sa médiatrice).
On peut sans problème utiliser directement cette propriété du cercle qu’il est cependant facile de démontrer.
\
[ ont même mesure ; il en est donc de même
En effet :le triangle OP A étant évidemment isocèle, les angles OP
Q et OAQ
\
[
pour P OQ et QOA . Les triangles OQA et OP A sont donc isométriques (deux côtés un angle) d’où AQ = QP. Dès lors
AQ = QP ⇒ Q appartient à la médiatrice de [AP ] et de même AO = OP donc O appartient à la médiatrice de [AP ] .Cette
médiatrice est donc bien la droite (OQ) .
Ainsi, les triangle OIA et OIP étant isométriques, leurs aires sont égales.
L’aire du secteur angulaite QOP , qui s’obtient en ajoutant l’aire du triangle OIP et l’aire du secteur angulaire hachuré est
\ (dont une mesure, isométrie oblige vaut
donc la même que celle du secteur angulaire intercepté par l’angle au centre QOP
22 × α
α). Cette aire vaut (voir exercice précédent A(α) =
⇒ A(α) = 2α
2
2. Ainsi A(α) = 4 si et seulement si α = 2 rad et en degrés α = 2 ×
180
360
donc α =
π
π
◦
Exercice 3 :
\ et ABE
\ ont même mesure. La somme des angles du triangle AEB valant π, on a :
ABE étant isocèle, les angles AEB
\
\ 2AEB
\ = π ⇒ AEB
\ = π − BAE
BAE+
2
⎧
π
\ + BAE
\=
⎨ CAB
2 ⇒ BAE
\= π −π = π
Or
\= π
⎩ CAB
2
3
6
3
π
π−
6 = 5π puis que BEH
\=
\= π
\ = π − AEB
\ ⇒ BEH
On en déduit que AEB
2
12
2
12
√
a 3
2. Soit a le côté du carré (donc AC = CD = DE = EA = a) La hauteur du triangle équilatéral vaut
2
Ã
Ã
√
√ !
√ !
a 3
2− 3
3
On en déduit que BH = a −
⇒ BH = a 1 −
⇒ BH = a
2
2
2
2
³
´
³ ´
\ = BH ⇒ tan π =
et dans le triangle rectangle EBH, tan BEH
EH
12
a
Ã
√ !
2− 3
√ ¢
¡
³π´
2
√
a 2− 3 2
=
tan
×
⇒
=2− 3
a
2
a
12
2
Exercice 4 :
1. a. On sait que pour tout réel x 6=
Ainsi, pour tout réel x 6=
sin (x)
π
+ kπ, tan(x) =
2
cos (x)
sin2 (x)
sin2 (x)
π
cos2 (x) + sin2 (x)
2
(x)
=
1
+
+ kπ, tan2 (x) =
⇒
1
+
tan
=
.
2
cos2 (x)
cos2 (x)
cos2 (x)
Or cos2 (x) + sin2 (x) = 1
π
1
+ kπ, 1 + tan2 (x) =
2
cos2 (x)
π
Propriété qui est donc valable pour x 6= + kπ (ne jamais diviser par 0)
2
sin (x)
1
π
et
est définie dès lors que tan(x) est définie et non nulle, c’est à
On a encore, pour tout réel x 6= , tan(x) =
2
cos (x)
tan(x)
π
dire pour x différent de + kπ ( tan définie) et différent de kπ (non nulle).
2
1.b. On a donc, pour tout réel x 6=
Dès lors,
cos2 (x)
sin2 (x) + cos2 (x)
1
cos (x)
1
1
=
1
+
=
=
=
⇒1+
sin (x)
tan(x)
sin (x)
tan2 (x)
sin2 (x)
sin2 (x)
cos (x)
On en déduit comme ci-dessus que 1 +
1
π
1
=
pour x 6= + kπ et x 6= kπ.
2
tan2 (x)
sin2 (x)
2. La donnée de la tangente ne suffit pas car 1 + tan2 (x) =
r
r
ou cos (x) = −
(x)
⇒ cos2 (x) =
1
1 + tan2 (x)
1
. Pour une même tangente, deux angles sont possibles.
1 + tan2 (x)
v
³π´ u
h πi
π
1
3. sachant que
∈ 0,
, son sinus et son cosinus sont positifs. Ainsi, cos
=u
t
π
12
2
12
1 + tan2 ( )
12
√
√ ¢2
√
¡
π
π
π
Or tan( ) = 2 − 3 ⇒ tan2 ( ) = 2 − 3 donc tan2 ( ) = 7 − 4 3
12
12
12
√
√
π
1
8+4 3
1
√
√ ¢ en multiplant par la quantité conjuguée.
√
¢
¡
¡
=
Donc 1 + tan2 ( ) = 8 − 4 3 et
=
π
12
8−4 3
8−4 3 8+4 3
1 + tan2 ( )
12
p√
p
r√
√
√
³π´
³π´
³π´
3+2
3+2
3+2
2− 3
1
cos
et
de
même
sin
et
cos
=
⇒
=
=
=
Ainsi,
π
4
12
4
12
2
12
2
1 + tan2 ( )
12
³π´
³
´
1
+
cos
1 + cos (2x)
π
6 .
4. cos (2x) = 2 cos2 (x) − 1 ⇒ cos2 (x) =
donc cos2
=
2
12
2
√
3
p
√
√
³π´
³ π ´ 1+
³ π ´ 2 + √3
³π ´
3
2+ 3
2
2
2
Or cos
=
donc cos
=
⇒ cos
=
⇒ cos
=
6
2
12
2
12
4
12
2
p
√
√
³π´
³π´
³π´
³ π ´ 2 − √3
2+ 3
2− 3
Puis sin2
= 1 − cos2
=1−
⇒ sin2
=
⇒ sin
=
12
12
4
12
4
12
2
Donc cos (x) =
1
1 + tan2 (x)
1
cos2
3