Dérivées, les formules Dérivées des fonctions usuelles Opérations

Dérivées, les formules Première S, cours
Dérivées des fonctions usuelles
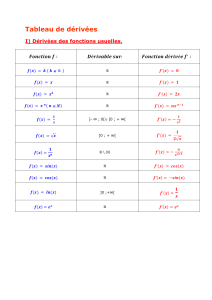
Ens. définition Fonctions Fonctions dérivées Ens. dérivabilité
Rx7→ koù k∈Rx7→ 0R
Rx7→ x x 7→ 1R
Rx7→ xn,n∈N∗x7→ n.xn−1,n∈N∗R
]− ∞; 0[∪]0; +∞[x7→ 1
xx7→ −1 x2Sur ]− ∞; 0[ et sur ]0; +∞[
]− ∞; 0[∪]0; +∞[x7→ 1
xn,n∈N∗x7→ −n xn+1 ,n∈N∗Sur ]− ∞; 0[ et sur ]0; +∞[
[0; +∞[x7→ √x x 7→ 1
2√x]0; +∞[
Rx7→ sin x,xest en radians x7→ cos xR
Rx7→ cos x,xest en radians x7→ −sin xR
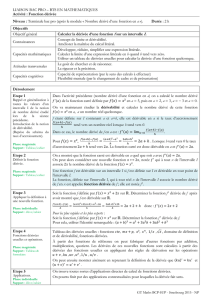
Opérations et dérivées
uet vsont deux fonctions dérivables sur I
Dérivée d’une somme (u+v)0=u0+v0
Dérivée du produit par une constante k(ku)0=ku0
Dérivée du produit (uv)0=u0v+uv0
Dérivée du carré de u(u2)0= 2uu0
Dérivée de un(un)0=nun−1.u0
Dérivée de l’inverse 1
v0
=−v0
v2
Dérivée du quotient u
v0
=u0v−v0u
v2
REMARQUE 1
•Un polynôme est dérivable sur R,
•Une fonction rationnelle est dérivable sur chacune des parties de son ensemble de définition.
Dérivée d’une fonction composée avec une fonction affine
THÉORÈME 1
Si fest une fonction dérivable sur un intervalle Iet si gest la fonction définie par g(x) = f(ax +b), alors g
est dérivable en tout point x, tel que ax +bappartient à Iet on a g0(x) = a×f0(ax +b).
Ens. définition Fonctions Fonctions dérivées Ens. dérivabilité
ax +b≥0x7→ √ax +b x 7→ a
2√ax +bax +b > 0
Rx7→ sin(ax +b)x7→ acos(ax +b)R
Rx7→ cos(ax +b)x7→ −asin(ax +b)R
http://ambali.net p. : 1 / 1