EXERCICE III L`eau distillée et son pH

TS3, TS5 et TS6 DS de PHYSIQUE CHIMIE
15/03/2016 2 h 00
remarque : La présentation sera soignée ; les résultats demandés encadrés . Tout résultat non justifié ne sera pas
pris en compte.
Chaque exercice sera rédigé sur une copie particulière . Le barème indiqué, peut être modifié lors de la
correction.
EXERCICE I : Le pH d'une eau distillée (10 points)
Le but de cet exercice est de comprendre pourquoi le pH d’une eau distillée laissée à l’air libre diminue.
1. pH de l’eau pure à 25 °C
1.1. Dans toute solution aqueuse se produit la réaction d’autoprotolyse de l’eau.
Écrire l’équation de cette réaction.
1.2. Exprimer la constante d’équilibre Ke associée à l’équation précédente. Quel nom donne-t-on à cette
constante Ke ?
1.3. À 25°C, des mesures de conductivité électrique montrent que pour de l’eau pure :
[H3O+]éq, = [HO ]éq = 1,0 10
7 mol.L 1 .
1.3.1 Calculer la valeur de Ke à 25 °C .
1.3.2 Calculer la valeur du pH de l’eau pure à 25 °C.
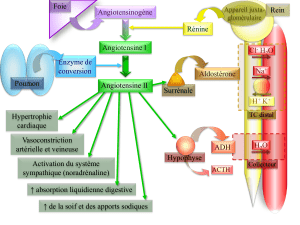
2. Eau distillée laissée à l’air libre
De l’eau fraîchement distillée et laissée quelque temps à l’air libre dans un bécher, à 25 °C, voit son pH diminuer
progressivement puis se stabiliser à la valeur de 5,7. La dissolution lente et progressive dans l’eau distillée du
dioxyde de carbone présent dans l’air permet d’expliquer cette diminution du pH. Un équilibre s’établit entre le
dioxyde de carbone présent dans l’air et celui qui est dissous dans l’eau distillée noté CO2, H2O.
Dans la suite de l’exercice on ne tiendra pas compte de la réaction entre les ions hydrogénocarbonate HCO3(aq)
et l’eau.
Le couple dioxyde de carbone dissous / ion hydrogénocarbonate est CO2, H2O / HCO3(aq).
2.1. L’équation de la réaction entre le dioxyde de carbone dissous et l’eau s’écrit :
CO2, H2O + H2O( ) HCO3 (aq) + H3O+.
Écrire les couples acido-basiques mis en jeu dans cette équation.
2.2. Exprimer la constante d’acidité KA associée à l’équation précédente.
2.3. Montrer qu’à partir de l’expression de KA on peut écrire :
pH = pKA + log ( [HCO3]éq / [CO2, H2O]éq ) relation (1 )
2.4. Sachant que pKA = 6,4 et en utilisant la relation (1), calculer la valeur du
quotient [HCO3]éq / [CO2, H2O]éq pour de l’eau distillée de pH = 5,7. Parmi les espèces
CO2, H2O et HCO3(aq) quelle est celle qui prédomine dans de l’eau distillée de pH = 5,7 ?
Justifier.
2.5. Tracer le diagramme de prédominance des espèces CO2, H2O et HCO3(aq).
2.6. Tableau d’avancement
2.6.1 Compléter littéralement le tableau d’avancement molaire donné en annexe en fonction de V
(volume considéré d’eau distillée) et de c (concentration molaire apportée en dioxyde de carbone de l’eau
distillée).
2.6.2 Quelle est la relation entre [HCO3]éq et [H3O+]éq? En déduire la valeur de [HCO3]éq.

2.6.3 Déterminer la valeur de [CO2, H2O]éq en utilisant l’expression de la constante d’acidité établie à la
question 2.2.
2.6.4 En déduire la valeur de c.
3. Influence de la composition atmosphérique
3.1. Dans un mélange gazeux, comme l’air, chacun des gaz qui le constitue contribue à la pression du mélange
proportionnellement à sa quantité de matière. C’est la pression partielle du gaz considéré.
Exemple : si l’air contient en quantité 20% de dioxygène alors la pression partielle du dioxygène, notée
O
p2
, vaut 20 % de la pression de l’air.
L’atmosphère terrestre possède actuellement un pourcentage moyen en quantité de CO2 de 0,038 %.
Pour une pression atmosphérique de 1,013  105 Pa, à quelle pression partielle
CO
p2
de CO2 ce
pourcentage moyen correspond-il ?
3.2. La concentration d’un gaz dissous dans l’eau est proportionnelle à sa pression partielle quand l’équilibre
du système chimique est atteint. Dans le cas du dioxyde de carbone on a :
[CO2, H2O]éq = k
CO
p2
avec k = 3,4 10
7 mol.L-1.Pa 1.
Pour un pourcentage moyen en quantité de CO2 de 0,038% et pour une pression atmosphérique de 1,013 
105 Pa, calculer la valeur de la concentration [CO2, H2O]éq dans une solution aqueuse quand l’équilibre
entre le dioxyde de carbone atmosphérique et le dioxyde de carbone dissous est atteint.
3.3. En comparant la valeur précédente à celle obtenue à la question 2.6.3., indiquer sans calcul si l’air du
laboratoire où a eu lieu la préparation de l’eau distillée possède un pourcentage en dioxyde de carbone plus
petit ou plus grand que 0,038 %.
4. L'eau minérale et sa teneur en ion hydrogénocarbonate :
On prélève un volume V1 = 20,0 mL d’eau minérale auquel est additionnée progressivement une solution
d’acide chlorhydrique ayant une concentration C = 1,0 × 10–2 mol.L-1.Selon la réaction suivante :
HCO3–(aq) + H3O+(aq) CO2, H2O(aq) + H2O(l)
Sur la figure de l’annexe sont indiqués les points expérimentaux du dosage, obtenus par suivi pH-métrique.
4.1. Définir l’équivalence lors du dosage des ions hydrogénocarbonate.
4.2. Déterminer les coordonnées du point d’équivalence par méthode graphique( faire
apparaitre les constructions sur la courbe).
4.3. Calculer la concentration molaire en ions hydrogénocarbonate dans cette eau minérale.
4.4. A partir de la courbe de titrage proposer une méthode permettant de déterminer rapidement
la valeur du pKA du couple : CO2, H2O / HCO3(aq).
Annexe question 4.2

Annexe question 2.6.1
Équation de la réaction
CO2, H2O + H2O ( ) HCO3(aq) + H3O+
État du système chimique
Avancement
(mol)
État initial
(mol)
0
solvant
0
0
État intermédiaire
(mol)
x
solvant
État final (à l’équilibre)
(mol)
xéq
solvant
EXERCICE II : TRAVAIL, ENERGIE ET OSCILLATIONS (10 POINTS)
Partie A : Le toboggan Aquatique
Un enfant glisse le long d’un toboggan de plage. On étudie son mouvement dans un référentiel terrestre
supposé galiléen.
Dans l’exercice, l’enfant sera assimilé à un point matériel noté G et on négligera tout type de frottement,
ainsi que toutes les actions dues à l’air.
- Une piste DO qui permet à l’enfant partant de D sans vitesse initiale et d’atteindre le point O avec
une vitesse Vo faisant un angle α avec l’horizontale (voir schéma ci-dessous) ;
- Une piscine de réception.
Données : masse de l’enfant m= 35 kg
L’intensité de la pesanteur g = 10 m.s-2 ;
Dénivellation h = 5,0 m.
On choisit l’altitude du point O comme référence pour l’énergie potentielle de pesanteur.
1. Donner l’expression de l’énergie potentielle de pesanteur Epp(D) de l’enfant au point D.
2. Donner l’expression de l’énergie mécanique Em(D) de l’enfant au point D. Justifier la réponse.
3. Donner l’expression de l’énergie mécanique Em(O) de l’enfant au point O.
4. En déduire l’expression de la valeur Vo de la vitesse en justifiant le raisonnement. Calculer sa
valeur.
5. En réalité la vitesse de l’enfant est nettement inférieure et vaut 6,0 m.s-1. Comment peut-on expliquer
cette différence ?
6. Calculer le travail des forces de frottement le long du trajet DO.

Partie B : Oscillation d'un pendule
1. Étude des oscillations du pendule simple.
On étudie un pendule simple constitué d’une masse ponctuelle m, attachée à l’une des extrémités d’un fil
inextensible, de masse négligeable et de longueur L.
Ce pendule est placé dans le champ de pesanteur dans le référentiel terrestre considéré comme galiléen.
Ecarté de sa position d'équilibre pour des angles θ inférieur à 20°, afin de vérifier l'isochronisme des petites
oscillations.
1.1. Définir le terme d'isochronisme des petites oscillations.
1.2. Faire l’analyse dimensionnelle des trois formules suivantes. En déduire l’expression de la période
propre des petites oscillations d’un pendule simple.
T0 =
2L
g
; T0 = 2
m
L
; T0 =
L
2g
.
1.3. Nous souhaitons réaliser un pendule de période une seconde, quelle est la valeur de la grandeur qu'il
faudra fixer pour accéder à la période de ce pendule ?
2. Étude énergétique d'un pendule pesant :
Un pendule pesant est constitué d'un solide de masse m, accrochée à une tige métallique de longueur L.
Ecarté de sa position d'équilibre, puis lâché sans vitesse initiale, à la date t = 0. Il oscille de part et d'autre de
sa position d'équilibre.
Le mouvement du pendule a été enregistré à l’aide d’un dispositif d'acquisition et d'un logiciel de traitement
permettant de tracer l'évolution des différentes formes d'énergie au cours du temps.
Rappeler l’expression en explicitant chaque terme :
2.1. Quelles sont les différentes formes d'énergie que possède le solide ?
2.2. En justifiant votre choix, attribuer l’énergie correspondant à chaque type de courbe ci-après.
2.3. Donner la valeur de la variation de l'énergie mécanique du solide pendant la durée de l'étude.
2.4. Quelle est l’origine de l' amortissement de ce pendule ? Que devient l’énergie perdue ?
2.5. Donner, en justifiant, la valeur du travail des actions mécaniques responsables de cette
dissipation d'énergie.
Annexe graphe question 2.2