Ch 8 Sommaire 0- Objectifs CERCLE ET POLYGONE RÉGULIER

Ch 8
Sommaire
0- Objectifs
1- Angle inscrit et angle au centre
2- Polygones réguliers
3- Calculs d'angles
0- Objectifs
• Connaître et utiliser la relation entre un angle inscrit et l’angle au
centre qui intercepte le même arc.
• Construire un triangle équilatéral, un carré, un hexagone régulier, un
octogone connaissant son centre et un sommet.
CERCLE ET POLYGONE RÉGULIER

1- Angle inscrit et angle au centre
Définition :
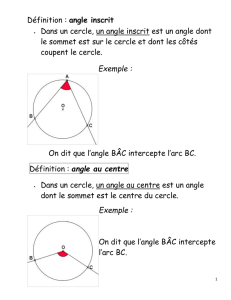
Dans un cercle, un angle inscrit est un angle dont le sommet est
un point du cercle et dont les côtés coupent le cercle.
Exemple :
A, S et B sont sur un même cercle donc
̂
ASB
est un angle inscrit.
Définition :
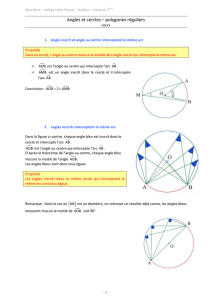
Dans un cercle, un angle au centre est un angle dont le sommet
est le centre du cercle.
Exemple :
A et B sont sur le cercle de centre O donc
̂
AOB
est un angle au
centre.
arc intercepté
arc intercepté

Théorème :
Dans un cercle, si un angle inscrit et un angle au centre
intercepte le même arc alors l'angle inscrit est égal à la moitié de
l'angle au centre.
Exemple :
L'angle au centre
̂
AOB
et l'angle inscrit
̂
ACB
intercepte le
même arc donc
̂
ACB
=
1
2
̂
AOB
Conséquence :
Dans un cercle, deux angles inscrits qui interceptent le même arc
sont égaux.
Exemple :
Les angles inscrits
̂
ACB
et
̂
ADB
interceptent le même arc d'un
même cercle donc
̂
ACB
=
̂
ADB
.
arc intercepté
arc intercepté

2- Polygones réguliers
Définition :
Un polygone régulier est un polygone dont les sommets sont sur
un même cercle et dont tous les angles au centre formés par
deux sommets consécutifs sont égaux.
Exemples : (voir le site du collège pour d'autres exemples)
À l'aide de la méthode de la rosace, on obtient un triangle
équilatéral et un hexagone régulier.
En traçant deux diamètres perpendiculaires, on obtient un carré.
Puis avec les bissectrices des angles au centre qui sont droits, on
obtient un octogone régulier.
Propriété :
Un polygone régulier a ses côtés égaux et ses angles égaux.

3- Calculs d'angles
* Avec le triangle équilatéral ci-dessus :
BDF est un triangle équilatéral inscrit dans un cercle de centre O
donc
^
FOB
=
360
°
3
= 120°
Par ailleurs, l'angle inscrit
^
FDB
et l'angle au centre
^
FOB
interceptent le même arc donc, d'après le théorème de l'angle
inscrit,
^
FDB
=
^
FDB
2
=
120
°
2
=60°
* Avec l'hexagone régulier ci-dessus :
ABCDEF est un hexagone régulier inscrit dans un cercle de
centre O
donc
^
AOB
=
360
°
6
= 60°
donc
^
AOE
= 4×
^
AOB
= 4×60° = 240°
Par ailleurs, l'angle inscrit
^
AFE
et l'angle au centre
^
AOE
interceptent le même arc donc, d'après le théorème de l'angle
inscrit,
^
AFE
=
^
AOE
2
=
240
°
2
=120°
* Avec l'octogone régulier ci-dessus :
AEBFCGDH est un octogone régulier inscrit dans un cercle de
centre O
donc
^
AOE
=
360
°
8
= 45°
donc
^
AOD
= 6×
^
AOE
= 6×45° = 270°
Par ailleurs, l'angle inscrit
^
AHD
et l'angle au centre
^
AOD
interceptent le même arc donc, d'après le théorème de l'angle
inscrit,
^
AHD
=
^
AOD
2
=
270
°
2
=135°