Angles inscrits – Polygones réguliers

Angles inscrits – Polygones réguliers Troisième
1 Angles inscrits et angles au centre
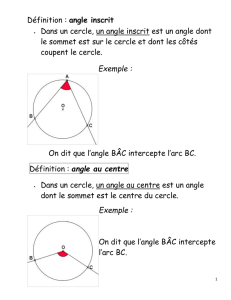
Définitions :
• Un angle inscrit dans un cercle est un angle dont le sommet est sur le cercle et dont les côtés coupent le cercle.
• Un angle au centre dans un cercle est un angle dont le sommet est le centre du cercle et dont les côtés coupent le
cercle.
Exemples :
Soit un cercle C de centre O et soit A et B deux points du cercle.
Soit C et D deux points de l’arc AB et soit E un point de l’arc È AB.
Les angles Æ ACB et Æ ADB sont des angles inscrits au cercle C
interceptant l’arc È AB.
L’angle saillant Æ AOB est l’angle au centre interceptant l’arc È AB.
L’angle Æ AEB est un angle inscrit à C interceptant l’arc AB.
L’angle rentrant AOB est l’angle au centre interceptant l’arc AB.
Propriétés : (Démonstration dans les activités 3 et 4 page 233)
• Si, dans un cercle, un angle au centre et un angle inscrit interceptent le même arc, alors la mesure de l’angle au
centre est le double de la mesure de l’angle inscrit.
• Si, dans un cercle, deux angles inscrits interceptent le même arc, alors ils ont même mesure.
Exemples : On reprend les exemples ci-dessus.
• L’angle inscrit Æ ACB et l’angle au centre Æ AOB interceptent le même arc È AB donc Æ AOB=2× Æ ACB.
L’angle inscrit Æ AEB et l’angle au centre AOB interceptent le même arc AB donc AOB=2× Æ AEB.
• Les angles inscrits Æ ACB et Æ ADB interceptent le même arc È AB, donc Æ ACB=Æ ADB.
Remarque : En prenant un angle au centre de 180°,
on retrouve une propriété vue en Quatrième.
2 Polygones réguliers
Définition :
Un polygone régulier est un polygone dont les côtés sont de même longueur et dont les angles sont de même mesure.
Exemples :
Triangle équilatéral Carré Pentagone régulier Hexagone régulier Heptagone régulier Octogone régulier
Propriété : (Admise)
Si un polygone est régulier, alors il est inscriptible dans un cercle.
Vocabulaire : Le centre du cercle circonscrit à un polygone régulier est appelé centre du polygone.
Propriété : (Admise)
Si un polygone à n côtés est régulier, alors la mesure de chaque angle au centre interceptant un côté est égale à
360°
n
.
Exemple :