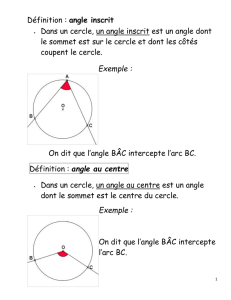
Exercices semaine du 09 au 13 mai

(
)
C
☺ Exercice p 256, n° 8 :
Dans la figure ci-dessous, les points A, B et C appartiennent au cercle
(
)
C
de centre I.
I
C
B
A
1) Reproduire la figure.
2) a) Colorer en rouge l’arc de cercle intercepté par l’angle inscrit
BAC
.
b) Marquer en bleu l’angle au centre qui intercepte le même arc de cercle que l’angle inscrit
BAC
.
3) Sachant que
65
BAC
= °
, déterminer, en justifiant, la mesure de l’angle
BIC
.
Correction :
1) 2) Figure :
I
C
B
A
65°
?
3) Mesure de l’angle
BIC
:
Dans le cercle
(
)
C
, l’angle inscrit
BAC
et l’angle au centre
BIC
interceptent le même arc
BC
(en rouge).
Or, d’après le théorème de l’angle inscrit, dans un cercle, si un angle inscrit et un angle au centre interceptent le
même arc, alors la mesure de l’angle inscrit est égale à la moitié de celle de l’angle au centre.
Donc :
1
2
BAC BIC
=
donc 2
BIC BAC
= ×
2 65
BIC
= ×
130
BIC
= °
.
L’angle
BIC
mesure donc 130°.

(
)
C
(
)
C
☺ Exercice p 256, n° 9 :
Dans la figure ci-dessous, les points A, B et C appartiennent au cercle
(
)
C
de centre I.
I
C
B
A
La mesure de l’angle
ACB
est égale à 55°.
Quel est l’angle au centre qui intercepte le même arc de cercle que l’angle inscrit
ACB
?
Déterminer, en justifiant, la mesure de cet angle au centre.
Correction :
I
C
B
A
55°
?
Mesure de l’angle
AIB
:
Dans le cercle
(
)
C
, l’angle inscrit
ACB
et l’angle au centre
AIB
interceptent le même arc
AB
(en vert).
Donc, d’après le théorème de l’angle inscrit :
1
2
ACB AIB
=
donc 2
AIB ACB
= ×
2 55
AIB
= ×
110
AIB
= °
.
L’angle
AIB
mesure donc 110°.

(
)
C
(
)
C
☺ Exercice p 256, n° 10 :
Dans la figure ci-dessous, les points P, M, N et R appartiennent à un même cercle
(
)
C
de centre O.
Déterminer, en justifiant, la mesure de l’angle
PNR
.
O
R
P
M
N
55°
Correction :
O
R
P
M
N
55°
?
Mesure de l’angle
PNR
:
Dans le cercle
(
)
C
, les angles inscrits
PMR
et
PNR
interceptent le même arc
PR
.
Or, dans un cercle, si deux angles inscrits interceptent le même arc, alors ils ont la même mesure.
Donc l’angle
PNR
a la même mesure que
PMR
, soit 55°.
☺ Exercice p 256, n° 11 :
Dans la figure ci-dessous, les points A, E, B et D appartiennent au cercle
(
)
C
de centre O.
1) Déterminer, en justifiant, la mesure de l’angle
ADB
.
2) Déterminer, en justifiant, la mesure de l’angle
AEB
.

(
)
C
(
)
C
O
E
B
D
A
80°
Correction :
O
E
B
D
A
80°
?
?
1) Mesure de l’angle
ADB
:
Dans le cercle
(
)
C
, l’angle inscrit
ADB
et l’angle au centre saillant
AOB
interceptent le même arc
AB
(en
vert).
Donc, d’après le théorème de l’angle inscrit :
1
2
ADB AOB
=
1
80
2
ADB
= ×
40
AOB
= °
.
L’angle
AOB
mesure donc 40°.
2) Mesure de l’angle
AEB
:
Dans le cercle
(
)
C
, l’angle inscrit
AEB
et l’angle au centre rentrant AOB interceptent le même arc
AB
(en
bleu).
Donc, d’après le théorème de l’angle inscrit :
1
2
AEB AOB
=
( )
1
360 80
2
AEB = × −
140
AEB
= °
.
L’angle
AEB
mesure donc 140°.

(
)
C
(
)
C
☺ Exercice p 258, n° 19 :
Dans la figure ci-dessous, les points R, P et M appartiennent au cercle
(
)
C
de centre O.
O
M
P
R
1) Reproduire la figure.
2) Marquer l’angle au centre et l’angle inscrit de sommet M qui interceptent le même arc de cercle
RP
.
3) Sachant que
65
ROP
= °
, déterminer, en justifiant, la mesure de l’angle
RMP
.
Correction :
1) 2) Figure :
O
M
P
R
65° ?
3) Dans le cercle
(
)
C
, l’angle inscrit
RMP
et l’angle au centre
ROP
interceptent le même arc
RP
(en vert).
Donc, d’après le théorème de l’angle inscrit :
1
2
RMP ROP
=
1
65
2
RMP
= ×
32,5
RMP
= °
.
L’angle
RMP
mesure donc 32,5°.