2nde-fonctions-homog.. - Mathématiques au lycée Bellepierre

Chapitre 11 – Fonctions homographiques TABLE DES MATIÈRES – page -1
Chapitre 11 – Fonctions homographiques
Table des matières
I Exercices I-1
1 ................................................ I-1
2 ................................................ I-1
3 ................................................ I-2
4 ................................................ I-2
5 ................................................ I-2
6 ................................................ I-2
7 Une courbe de fonction homographique en détail . . . . . . . . . . . . . . . . . . . . . I-3
8 ................................................ I-4
9 ................................................ I-4
10 ................................................ I-4
11 ................................................ I-4
12 ................................................ I-4
13 ................................................ I-5
14 ................................................ I-6
15 ................................................ I-6
16 ................................................ I-6
II Cours II-1
1 Rappels – Inverse d’un nombre . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . II-1
2 Fonctioninverse.......................................II-1
3 Fonctions homographiques . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . II-1
3a Définition et exemples . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . II-1
3b Ensemble de définition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . II-2
3c Antécédent d’un nombre par une fonction homographique . . . . . . . . . . . II-2
3d Signe d’une fonction homographique et inéquation . . . . . . . . . . . . . . . . II-2
2de – Mathématiques TDM http://www.maths.lyceebellepierre.fr

Chapitre 11 – Fonctions homographiques I EXERCICES – page I-1
I Exercices
Fonction inverse
1
La fonction fest définie par f(x) = 1
x, on l’appelle la fonction inverse parce que 1 xest l’inverse de x.
1. Compléter le tableau ci-dessous par des nombres décimaux.
x−5−4−2−1−0,5−0,2 0 0,2 0,5 1 2 4 5
1
x
2. Tracer ci-dessous la représentation graphique de la fonction f.
3. Dresser le tableau de variation de la fonction inverse.
4. La fonction inverse est-elle linéaire ? affine ? Justifier.
1
2
3
4
−1
−2
−3
−4
−5
1 2 3 4−1−2−3−4−5
2
Répondre aux questions ci-dessous en donnant les valeurs exactes.
1. Par la fonction inverse, quelle est l’image
(a) de 7 ? (b) de 2
3? (c) de −100 ? (d) de −0,3 ? (e) de 106? (f) de 10−5?
2. Par la fonction inverse, un seul nombre n’a pas d’image. Lequel ?
3. Par la fonction inverse, quel est l’antécédent
(a) de 7 ? (b) de 2
3? (c) de −100 ? (d) de −0,3 ? (e) de 106? (f) de 10−5?
4. Par la fonction inverse, un seul nombre n’a pas d’antécédent. Lequel ?
5. Si x6= 0, quel est l’inverse de 1
x?
2de – Mathématiques TDM http://www.maths.lyceebellepierre.fr

Chapitre 11 – Fonctions homographiques I EXERCICES – page I-2
3
Donner les solutions exactes des équations suivantes :
(a) 1
x= 9 (b) 1 x=−5 7(c) 1 x= 1,3 (d) 1 x=√2 2
4
Sur l’intervalle [0 ; +∞[, la fonction inverse
1. admet-elle un minimum ?
2. admet-elle un maximum ?
5
1. a) Compléter par le signe < ou > sans effectuer de calcul : 6,9...7 donc 1
6,9...1 7
b) Citer la propriété de la fonction inverse utilisée ci-dessus, en précisant l’intervalle.
2. a) Compléter par le signe < ou > sans effectuer de calcul : −9...−6 donc 1
−9... 1 −6
b) Citer la propriété de la fonction inverse utilisée ci-dessus, en précisant l’intervalle.
3. a) Compléter par le signe < ou > : −2...41
−2...1 4
b) Peut-on dire que la fonction inverse est décroissante sur ] − ∞ ; 0[ ∪]0 ; +∞[ ?
6
Dans chaque cas, compléter par le signe < ou > sans effectuer de calcul.
(1) 1
13 ... 1 13,02 (2) 1 5,3... 1 5,28 (3) 1 −7... 1 −7,3
(4) 1
−0,37 ... 1 −0,3(5) 1
3 + √2... 1 5 + √2(6) 1
π+ 1 ... 1 π
2de – Mathématiques TDM http://www.maths.lyceebellepierre.fr

Chapitre 11 – Fonctions homographiques I EXERCICES – page I-3
Fonctions homographiques
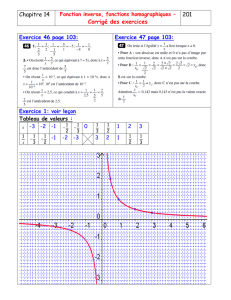
7 Une courbe de fonction homographique en détail
On considère la fonction définie par f(x) = −2x+ 4
x−3.
1. a) Calculer l’image de 5 par la fonction f.
b) Écrire le calcul détaillé de la calculatrice.
2. Compléter les tableaux de valeurs ci-dessous. Arrondir au 10e.
3. Pour une certaine valeur de x, on constate que f(x) n’est pas définie (n’existe pas). Pour
quelle valeur de x?
4. Tracer soigneusement la représentation graphique de la fonction fdans le repère de la page
suivante.
5. Dresser le tableau de variation de la fonction f.
x−4−2 0 1 1,5 2 2,5 2,7
f(x)
x3 3,3 3,5 4 4,5 5 7 10
f(x)
1
2
3
4
−1
−2
−3
−4
−5
−6
−7
−8
−9
123456789−1−2−3−4
2de – Mathématiques TDM http://www.maths.lyceebellepierre.fr

Chapitre 11 – Fonctions homographiques I EXERCICES – page I-4
8
La fonction fest définie par f(x) = 2x+ 5
x−4.
1. a) L’image de 3 par la fonction fest-elle définie (existe-t-elle) ?
b) Si la réponse est oui, calculer en détaillant l’image de 3 par f.
2. Mêmes consignes a) et b) pour les nombres : 4 ; −4 ; −6 ; −2,5.
9
Même exercice que l’exercice 8 pour la fonction fdéfinie par f(x) = 3x−5
x+ 2 , et pour 1 3, puis 5 3.
Si l’image existe, il faut en donner la valeur exacte.
10
1. Déterminer l’ensemble de définition de la fonction fdéfinie par f(x) = 1
x
2. Même question dans chacun des cas suivants : (a) f(x) = −2x+ 4
x−3(b) f(x) = 4x−3 x−5
(c) f(x) = 2x
x+ 4 (d) f(x) = x−3 x(e) f(x) = −4 2x+ 3 (f) f(x) = 2x+ 7 3x−5
11
La fonction fest définie par f(x) = 3x−2
x+ 1 .
Répondre aux questions suivantes en détaillant et en donnant les valeurs exactes.
1. Calculer les images de 9 et de −4.
2. Calculer les antécédents de 5 et de −6.
12
La fonction fest définie par f(x) = 3x+ 4
x−1
1. Déterminer l’ensemble de définition de la fonction f.
2. Avec la calculatrice, tracer la courbe de la fonction f sur l’intervalle [−8 ; 8].
3. Dresser le tableau de variation de la fonction f
4. Résoudre l’équation f(x) = 6
(a) graphiquement avec la calculatrice ; (b) algébriquement.
5. La fonction g est définie par g(x) = 2x−4
a) Tracer la représentation graphique de la fonction à la calculatrice dans le même repère.
b) Résoudre l’équation f(x) = g(x) graphiquement à la calculatrice.
c) Résoudre l’équation f(x) = g(x) algébriquement.
2de – Mathématiques TDM http://www.maths.lyceebellepierre.fr