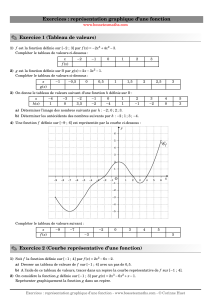
Dans cet exercice, il n`est pas demandé de justifier la dérivabilité

1S DS no6Dur´ee :2h
Exercice 1 ( 4 points )
Dans cet exercice, il n’est pas demand´e de justifier la d´erivabilit´e des fonctions ´etudi´ees.
La fonction fest d´efinie sur Rpar f(x) = 3x4+ 4x3+ 30x2−84x+ 2
1. La fonction gest d´efinie sur Rpar g(x) = 3x3+ 3x2+ 15x−21.
D´eterminer le signe de g(x) avec la m´ethode de votre choix (traiter une seule des deux questions
ci-dessous)
a) M´ethode 1 : Calculer g0(x) et ´etudier dresser le tableau de variation de g. Calculer g(1) et en d´eduire le
signe de g(x)
*Solution:
Non demand´e : gest d´erivable sur R(somme de fonctions d´erivables sur R)
g0(x) = 3 ×3x2+ 3 ×2x+ 15x−0 = 9x2+ 6x+ 15
g0(x) = 9x2+ 6x+ 15
Signe de g0(x)
∆ = b2−4ac = 62−4×9×15 = −504
∆<0 donc le 9x2+ 6x+ 15 n’admet aucune racine et est du signe de a= 9 coefficient de x2
donc g0(x)>0
Tableau de variation de g:
b) Calculer g(1) et en d´eduire le signe de g(x)
*Solution:
g(1) = 3 ×13+ 3 ×12+ 15 −21 = 21 −21 = 0.
g(1) = 0
On a alors :
On peut en utilisant le tableau de variation de gen d´eduire le signe de g(x) :
g(x)<0 sur ] − ∞; 1[ et g(x)>0 sur ]1; +∞[

Remarque
La justification du signe de g(x) avec le tableau de variation est ainsi incompl`ete car elle suppose
que gest strictement croissante(prouv´e avec le signe de g0(x)) mais aussi que gest continue sur R
(graphiquement, la courbe repr´esentative de gest un ”trait continu” et peut ˆetre trac´ee sans lever le
crayon).
c) M´ethode 2 : Calculer g(1) puis d´eterminer a,bet ctel que g(x) = (x−1)(ax2+bx +c) et en d´eduire le
signe de g(x)
*Solution:
g(1) = 3 ×13+ 3 ×12+ 15 −21 = 21 −21 = 0.
On peut donc factoriser par x−1 et pour tout r´eel x,g(x) peut s’´ecrire sous la forme g(x) =
(x−1)(ax2+bx +c) avec a,bet cr´eel.
g(x) = (x−1)(ax2+bx +c) = ax3−ax2+bx2−bx +cx −c= 3x3+ 3x2+ 15x−21
Par identification des coefficients :
a= 3
b−a= 3 ⇐⇒ b= 3 + a= 6
et −c=−21 ⇐⇒ c= 21
donc g(x) = (x−1)(3x2+ 6x+ 21)
Etude du signe de 3x2+ 6x+ 21 :
∆=62−4×3×21 = −216
∆<0 donc il n’y a pas de racines et 3x2+ 6x+ 21 est de signe constant et du signe de a= 3
coefficient de x2
donc 3x2+ 6x+ 21 >0
g(x) est donc du signe de x−1 soit g(x)>0 pour x > 1etg(x)<0 pour x < 1
Remarque
Il est possible d’utiliser ´egalement la division de polynˆomes (hors programme) pour obtenir a,b
et c.
2. Calculer f0(x) et en d´eduire les variations de f
*Solution:
Non demand´e : fest d´erivable sur R(somme de fonctions d´erivables dur R
f0(x) = 3 ×4x3+ 4 ×3x2+ 30 ×2x−84 + 0 = 12x3+ 12x2+ 60x−84
f0(x) = 12x3+ 12x2+ 60x−84
g(x) = 3x3+ 3x2+ 15x−21
f0(x) = 12x3+ 12x2+ 60x−84 = 4(3x3+ 3x2+ 15x−21) = 4g(x)
donc f0(x) est du mˆeme signe que g(x)
On a alors f0(x)<0 sur ] − ∞; 1[ et g(x)>0 sur ]1; +∞[
donc fest strictement d´ecroissante sur sur ] − ∞; 1[ et strictement croissante sur ]1; +∞[
Remarque
On peut aussi dresser le tableau de variation de f(pas demand´e) pour r´epondre `a la question mais
il faut alors calculer f(1)
f(1) = 3 + 4 + 30 −84 + 2 = −45

Exercice 2 ( 5 points )
On consid`ere la fonction fd´efinie sur [−10; 10] par f(x) = x−1
x2+ 3
et on note Cfsa courbe repr´esentative partiellement trac´ee dans le rep`ere orthogonal ci-dessous.
1. Apr`es avoir justifi´e la d´erivabilit´e de fsur [−10; 10], calculer f0(x) et dresser le tableau de variation de f.
On donnera les valeurs exactes des extremums.
*Solution:
On pose u(x) = x−1etv(x) = x2+ 3
uet vsont d´erivables sur Rdonc sur [−10; 10]
donc f, quotient de uet v, est d´erivable sur [−10; 10]
u(x) = x−1etv(x) = x2+ 3
donc on a u0(x) = 1 et v0(x) = 2x
f0(x) = u0(x)v(x)−u(x)v0(x)
(v(x))2
=1(x2+ 3) −(x−1)(2x)
(x2+ 3)2
=x2+ 3 −2x2+ 2x
(x2+ 3)2
=−x2+ 2x+ 3
(x2+ 3)2
f0(x) = −x2+ 2x+ 3
(x2+ 3)2
(x2+ 3)2>0 sur [−10; 10] donc f0(x) est du signe de −x2+ 2x+ 3
Racines et signe de −x2+ 2x+ 3
∆ = b2−4ac = 4 −4×(−1) ×3 = 16
∆>0 donc il y a deux racines :
x1=−b−√∆
2a=−2−4 −2= 3
et
x2=−b+√∆
2a=−2+4 −2=−1
f0(x) est du signe de a=−1 `a ”l’ext´erieur” des racines donc on a :

avec f(−10) = −10 −1
(−10)2+ 3 =−11 103 ,f(−1) = −1−1 (−1)2+ 3 =−2 4=−1 2
f(3) = 3−1
32+ 3 =2 12 =1 6et f(10) = 10 −1 102+ 3 =9 103
2. D´eterminer l’´equation r´eduite de la tangente T `a Cfau point A d’abscisse 1.
*Solution:
f0(1) = −12+2+3
(12+ 3)2=4 16 =1 4
f(1) = 1−1
12+ 3 = 0
T : y=f0(1)(x−1) + f(1) = 1
4(x−1) + 0 = x−1 4
T a pour ´equation r´eduite y=x−1
4
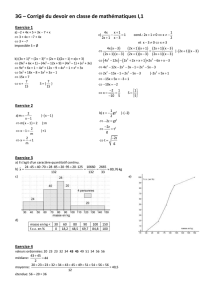
3. Compl´eter le trac´e de Cfdans le rep`ere ci-dessous en tra¸cant les tangentes parall`eles `a l’axe des abscisses
et la droite T.
*Solution:
Il faut avant tout placer les deux points correspondants aux extremums atteints en x=−1 et x= 3
et les tangentes parall`eles `a l’axe des abscisses en ces deux points puisque f0(−1) = f0(3) = 0 (coefficient
directeur de ces tangentes).
Pour tracer T, on peut chercher les coordonn´ees de deux points de T :
le point de coordonn´ees (1 ;0) est le point de contact entre la courbe et la tangente et si x= 0, y=−1
4
Exercice 3 ( 5 points )
ABCD est un carr´e de cˆot´e 4cm.
Pour tout Mde [AB], on nomme Ile point d’intersection
de [DM] et [AC].
xest la distance AM et A(x) est l’aire totale des deux tri-
angle AMI et DIC.

1. Calculer A(0) et A(4)
*Solution:
Si x= 0, les points I, M et A sont confondus
et donc A(0) est l’aire du triangle ACD
donc A(0) = 42
2= 8 cm2
A(0) = 8 cm2
Si x= 1, B, M et I sont confondus
et donc A(1) est l’aire du triangle BCD
donc A(1) = A(0) = 8 cm2
A(1) = 8 cm2
2. Soit hla hauteur issue de I dans AMI.
Montrer, en utilisant Thal`es, que IM
ID =x 4et que IM ID =h 4−h
En d´eduire que h
4−h=x 4et que h=4x x+ 4
*Solution:
ABCD est un carr´e
donc (AB)//(CD) et (AC) et (BD) sont s´ecantes en I
donc d’apr`es le th´eor`eme de Thal`es, on a :
IA
IC =IM ID =AM CD
or AM =xet CD = 4
donc IM
ID =x 4
et G∈(CD) et H∈(AB)
donc (DG)//(AH) et les droites (M D et (HG) sont concourantes en I
donc d’apr`es le th´eor`eme de Thal`es, on a :
IM
ID =IH IG =AH GD
IM =h,HG = 4 −IH = 4 −h
donc IM
ID =h 4−h
donc IM
ID =x 4=h 4−h
x
4=h 4−h
⇐⇒ x(4 −h) = 4h
⇐⇒ 4x−hx = 4h
⇐⇒ 4x=hx + 4h
⇐⇒ 4x=h(x+ 4)
⇐⇒ 4x
x+ 4 =h
h=4x
x+ 4