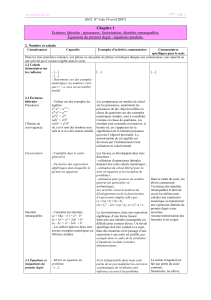
Expressions littérales

Collège Elie COUTAREL
Année 2008-2009.
G.MANDALLAZ.
Ecrit avec L
A
T
EX
Expressions littérales
1 Définition
Définition 1
Une expression littérale (ou expression algébrique) est une expression mathématique qui contient une ou plusieurs
lettres.
Exemple 1
Considérons E= 3x+ 7 et F= 7y−3x+ 12.
Eet Fsont des expressions littérales.
Remarque 1
Pourquoi utiliser des lettres ?
Il faut avoir en tête que ces lettres représentent des nombres, ces nombres peuvent être inconnus.
On est donc amenés à résoudre des problèmes où il faut trouver une ou des valeurs particulières de ces nombres
inconnus (on appelle cela résoudre une équation).
Mais avant cela il faut savoir manipuler ces expressions littérales.
Exemple 2
En géométrie, vous connaissez déjà quelques expressions littérales :
lL’aire d’un rectangle : Arectangle =L×l.
lLe périmètre d’un rectangle : Prectangle = 2 ×(L+l).
lL’aire d’un carré : Acarré =c×c=c2.
lLe périmètre d’un carré : Pcarré = 4 ×c.
lL’aire d’un disque : Adisque =π×r2.
lLe périmètre d’un cercle : Pcercle = 2 ×π×r.
Remarque 2
L’exemple précédent montre une autre utilité des expressions littérales : donner une forme générale à une formule
ou une propriété.
1

2 Manipulation des expressions littérales
2.1 Abstraction du signe "multiplier"
Dans certaines situations, on peut ne pas écrire le signe ×dans une expression algébrique.
1. Lorsqu’un nombre est placé devant une lettre.
Exemple 1 : 2×x= 2x.
Exemple 2 : 7
5×a=7 5a.
2. Entre deux lettres.
Exemple 1 : x×y=xy.
Exemple 2 : a×b=ab.
3. Devant une parenthèse.
Exemple 1 : 3×(2 + y) = 3(2 + y).
Exemple 2 : a×(x+b) = a(x+b).
Exemple 3
Les formules de géométrie deviennent donc :
lArectangle =Ll.
lPrectangle = 2(L+l).
lAcarré =c×c=c2.
lPcarré = 4c.
lAdisque =πr2.
lPcercle = 2πr.
2.2 Réduire et ordonner une expression littérale
Définition 2
Réduire une expression c’est regrouper les termes de même famille.
Exemple 4
F3x+ 7y+3+5y+ 2x+ 4 = 5x+ 12y+ 7.
F3x2+ 5y−2 + x+ 2y+ 6x+ 4 = 3x2+ 7y+ 7x+ 2.
Définition 3
Ordonner une expression c’est classer les termes dans un certain ordre (en principe l’ordre alphabétique).
2

2.3 Tester une égalité
Avant tout, il faut savoir substituer une valeur à une lettre :
Exemple 5
Considérons l’éxpression
E= 5x2−7x+ 4
Cherchons la valeur de Epour x= 3.
E= 5 ×32−7×3+4
E= 5 ×9−21 + 4
E= 45 −21 + 4
E= 28
Ici il est imératif de marquer les signes ×.
Nous allons maintenant tester si un nombre est une éventuelle solution d’une équation.
Exemple 6
Considérons l’équation
7x−4 = 5x+ 2
Le but est de trouver la (ou les) valeur(s) de xpour laquelle (lesquelles) l’égalité fonctionne.
Dans un premier temps, on va se contenter de tester quelques valeurs :
lTestons avec x= 4.
Membre de gauche : 7×4−4 = 28 −4 = 24.
Membre de droite : 5×4 + 2 = 20 + 2 = 22.
Le membre de gauche est différent de celui de droite, 4 n’est donc pas une solution de l’équation.
lTestons avec x= 3.
Membre de gauche : 7×3−4 = 21 −4 = 17.
Membre de droite : 5×3 + 2 = 15 + 2 = 17.
Le membre de gauche est égal de celui de droite, 3 est donc une solution de l’équation.
3