METHODE : RELATIONS MATHEMATIQUES, MANIPULATION ET

METHODE : MANIPULATION ET INTERPRETATION DES EXPRESSIONS LITTERALES.
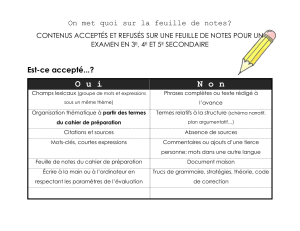
 Lors de cette séance, le travail est individuel et doit se faire en autonomie. Vous rédigerez les exercices sur une feuille à
part.
 Traitez un exercice de la première série. Faites valider la réponse par le professeur. Si la réponse est fausse, corrigez-la et
faites un exercice de la même série. Si la réponse est correcte, passez aux exercices de la série suivante.
EXERCICES SERIE 1 :
1. Association de lentilles et triangulation.
a) Les lentilles comme celles utilisées pour fabriquer des lunettes sont caractérisées par un nombre : la vergence.
La vergence C d’un ensemble de lentilles de vergences C1 et C2 accolées est donnée par la relation : C = C1 +
C2. Exprimez C2 en fonction de C et C1.
b) On donne la relation :
L
l
=
H
h
. Exprimez H en fonction de l, L et h.
2. Loi des tensions et triangulation.
a) La loi d’additivité des tensions s’écrit : UAB = UAC + UCB. Exprimez UAC en fonction de UAB et UCB.
b) On donne la relation :
n
m
=
d
h
. Exprimez n en fonction de m, h et d.
3. Loi des intensités et triangulation.
a) La loi des nœuds (ou d’additivité des intensités) s’écrit : I1 + I2 = I3 + I4. Exprimez I2 en fonction de I1 , I3 et I4
b) On donne la relation :
p
f
=
h
d
. Exprimez h en fonction de f, d et p.
EXERCICES SERIE 2 :
1. On donne une expression de la deuxième loi de Descartes sur la réfraction : n2.sin i = n1.sin r . Donner les
expressions littérales de n2 et sin r.
2. On donne une expression de la deuxième loi de Descartes sur la réfraction : nair.sin i1 = nverre.sin i2 . Donner les
expressions littérales de nair et nverre.
EXERCICES SERIE 3 :
1. On donne l’expression de la masse volumique µ d’un corps de masse m et de volume V :
µ
=
V
m
.
a. A masse m constante, comment évolue µ si le volume V augmente ?
b. A volume V constant, comment évolue µ si la masse m augmente ?
c. Donner les expressions littérales de m puis de V.
d. Calculer la masse volumique en g/cm3 d’un corps de masse m = 1,0 kg et de volume V = 1,00 L.
2. On donne l’expression de la vitesse v d’un mobile parcourant une distance d en une durée t :
v
=
t
d
.
a. A durée t constante, comment évolue v si la distance d diminue ?
b. A distance d constante, comment évolue v si la durée t diminue ?
c. Donner les expressions littérales de d puis de t.
d. Calculer la vitesse en m/s d’un mobile parcourant d = 3600 km en une durée t = 1,00 h.
3. On donne l’expression de la tension U aux bornes d’un conducteur ohmique de résistance R et parcouru par un
courant d’intensité I :
U
=
IR
.
a. Comment évolue la tension U si la résistance R augmente ?
b. Donner l’expression littérale de I.
c. La tension U restant constante, comment évolue l’intensité I si la résistance R augmente ?
d. Donner l’expression littérale de R.
e. Calculer la tension aux bornes d’un conducteur ohmique de résistance 330Ω (rappel : 1 Ω = 1V/A) parcouru par
un courant d’intensité I = 12 mA.
EXERCICES SERIE 4 :
1. La vitesse v d’un mobile qui a parcouru une distance d entre les temps t1 et t2 est donnée par la relation :
v
=
12 tt d
. Donner les expressions littérales de d, t1 et t2.
2. On donne la relation :
L
l
=
dDD
. Donner les expressions littérales de l, L, d et D.
3. On donne la relation :
H
h
=
LpL
. Donner les expressions littérales de L, h, H et p.