TS 2, Contrôle no 5

TS 2, Contrôle no5
Jeudi 29 mars 2012 2 heures
Exercice no1 Amérique du Sud, 16 novembre 2011 8 points
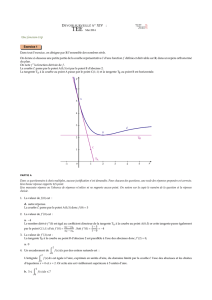
On considère la fonction gdéfinie sur l’intervalle ]0 ; +∞[ par : g(x)=x2(1 −lnx).
Partie A Étude de la fonction : g
1. Déterminer la limite de gen +∞.
2. Déterminer la limite de gen 0.
3. Étudier les variations de la fonction gsur l’intervalle ]0 ; +∞[.
4. En utilisant les résultats précédents, étudier le signe de la fonction gsur l’intervalle ]0 ; +∞[.
Partie B : Représentation graphique et aire sous la courbe
Soit Cla courbe représentative de la fonction g.
1. Tracer Cdans le repère orthonormal ayant pour unité graphique 4 cm.
2. Déterminer une équation de la tangente à la courbe Cau point A d’abscisse 1. La tracer sur le gra-
phique.
3. Soit G la fonction définie sur ]0; +∞[ par G(x)=1
3x3µlnx−1 3¶. Calculer G0(x).
4. Calculer l’aire en unités d’aire du domaine délimité par la courbe C, l’axe des abscisses et les droites
d’équations respectives x=1 et x=e.
Exercice no2 Nouvelle-Calédonie, mars 2012 12 points
Soit fla fonction définie sur [0 ; 1] par f(x)=xex.
On désigne par Cla courbe représentative de fdans le plan muni d’un repère orthogonal (O;~ ı;~ ).
Soit aun nombre réel appartenant à l’intervalle [0 ; 1].
Sur la courbe C, tracée en annexe, on a placé les points A et B d’abscisses respectives aet 1. On a tracé les
segments [OA] et [AB]. On a hachuré la partie du plan délimitée par les segments [OA] et [AB] et la courbe
C. On a placé les points A0(a; 0) et B0(1 ; 0).
Le but de l’exercice est de déterminer la valeur du nombre réel apour laquelle l’aire de la partie du plan
hachurée en annexe est minimale.
1

PARTIE A
1. Soit φla fonction définie par : φ(x)=xex−ex. Calculer la dérivée de φ. En déduire que Z1
0xexdx=1.
2. a) Donner l’aire du triangle OAA0.
Montrer que l’aire du trapèze ABB0A0est égale à 1
2¡−a2ea+aea−ae+e¢.
b) En déduire que l’aire de la partie du plan hachurée est égale à 1
2(aea−ae+e−2).
PARTIE B
Soit gla fonction définie sur [0 ; +∞[ par [g(x)=x(ex−e)+e−2.
1. Soit g0la fonction dérivée de la fonction g. Calculer g0(x) pour tout réel xde [0 ; +∞[.
Vérifier que la fonction dérivée seconde g00 est définie sur [0 ; +∞[ par g00(x)=(2+x)ex.
2. En déduire les variations de la fonction g0sur [0 ; +∞[.
3. Établir que l’équation g0(x)=0 admet une solution unique αdans l’intervalle [0 ; +∞[.
Déterminer une valeur approchée de αà 10−1près.
4. En déduire les variations de la fonction gsur [0 ; +∞[.
5. En utilisant les réponses aux questions des parties A et B, montrer qu’il existe une valeur de apour
laquelle l’aire de la partie du plan hachurée est minimale. Donner cette valeur de a.
Annexe
CETTE PAGE N’EST PAS À RENDRE AVEC LA COPIE
0 0,2 0,4 0,6 0,8 1 x
y
0
0,5
1
1,5
2
2,5
3
a
A
B
A0B0

Contrôle no5, Correction
On considère la fonction gdéfinie sur l’intervalle ]0 ; +∞[ par
g(x)=x2(1−lnx).
Partie A Étude de la fonction : g
1. Limite de gen +∞ :
lim
x→+∞g(x)=−∞, car lim x→+∞x2=+∞ et lim x→+∞1−lnx=−∞
2. Limite de gen 0 : On a g(x)=x2−x2lnx.
lim
x→0¡x2−x×xlnx¢=0, car lim x→0x=lim x→0x2=0 et lim x→0xlnx=0
3. Variations de la fonction gsur l’intervalle ]0 ; +∞[ :
gest dérivable sur ]0 ; +∞[, car produit de sommes de fonctions dérivables sur ]0 ; +∞[ et sur cet
intervalle :
g0(x)=2x(1−lnx)+x2×µ−1
x¶=2x−2xlnx−x=x−2xlnx=x(1−2ln x)
g0(x) est du signe de 1−2ln xpuisque xest positif.
g0(x)>0⇐⇒1−2lnx>0⇐⇒1>2lnx⇐⇒ 1
2>lnx⇐⇒e1
2=pe>x
g0(x)<0⇐⇒1−2lnx<0⇐⇒1<2lnx⇐⇒ 1
2<lnx⇐⇒ x<e1
2=pe
Sur ¤0 ; pe£la fonction est croissante
Sur ¤pe ; +∞£la fonction est décroissante
Pour x=peCpossède une tangente horizontale
x
g0(x)
g(x)
0pe+∞
+0−
00
1
2e
1
2e
−∞−∞
e
0
4. Signe de la fonction gsur l’intervalle ]0 ; +∞[ :
Sur ¤0 ; pe£,gest croissante, donc g(x)>0 et ne s’annule donc pas.
Sur ¤pe ; +∞£,gest décroissante et continue de 1
2e vers −∞.
Elle réalise donc une bijection de¤pe ; +∞£sur ¤−∞;1
2e£30. Elle s’annule donc une seule fois.
g(x)=0⇐⇒ x2(1−lnx)=0⇐⇒1−lnx=0 (puisque x6=0) ⇐⇒1=lnx⇐⇒ x=e
Conclusion : la fonction gest positive sur ]0 ; e[ et négative sur ]e ; +∞[.

Partie B : Représentation graphique et aire sous la courbe
Soit Cla courbe représentative de la fonction g.
1. Voir l’annexe 1.
2. Équation de la tangente à la courbe Cau point A d’abscisse 1.
On a g(1) =12(1 −ln1) =1.
Le cœfficient directeur de la tangente à la courbe Cau point d’abscisse 1 est le nombre dérivé f0(1) =
1(1−2ln1) =1.
Une équation de la tangente T à la courbe Cau point d’abscisse 1 est donc :
M(x;y)∈(T) ⇐⇒ y−g(1) =g0(1)(x−1) ⇐⇒ y−1=x−1⇐⇒ y=x
3. Dérivée de G(x) :
G0(x)=x2µlnx−1
3¶+1 3x3×1 x=x2lnx
Une primitive de x→x2ln xest donc G(x).
4. Aire en unités d’aire du domaine délimité par la courbe C, l’axe des abscisses et les droites d’équations
respectives x=1 et x=e :
On a vu que la fonction gest positive sur ]0 ; e[, donc sur ]1 ; e[.
L’aire, en unités d’aire de la surface délimitée par la courbe C, l’axe des abscisses et les droites d’équa-
tions respectives x=1 et x=e est donc égale à l’intégrale :
A=Ze
1x2(1−lnx)dx=Ze 1x2dx−Ze 1x2lnxdx
A=·x3
3¸e
1−[G(x)]e
1=·x3
3¸e
1−·1
3x3µlnx−1 3¶¸e
1=µe3
3−1 3¶−µe3 3µ1−1 9¶−1 3µ−1 3¶¶=e3−4 9
Exercice no2 Nouvelle-Calédonie, mars 2012 12 points
Soit fla fonction définie sur [0 ; 1] par f(x)=xex.
On désigne par Cla courbe représentative de fdans le plan muni d’un repère orthogonal (O;~ ı;~ ).
Soit aun nombre réel appartenant à l’intervalle [0 ; 1].
PARTIE A
1. Soit φla fonction définie par : φ(x)=xex−ex.
Dérivée de φ:
φ0(x)=ex+xex−ex=xex
Donc la fonction φest une primitive de xex. Ainsi :
Z1
0xexdx=£xex−ex¤1
0=(e−e)−(0 −1) =1
2. a) Aire A1du triangle OAA0,µbase ×hauteur
2¶:
La base a pour longueur a, la hauteur, aea; l’aire est donc : A1=a2ea
2.

Aire A2du trapèze ABB0A0µ(petite base+grande base)×hauteur
2¶:
La petite base AA0a pour longueur aea, la grande base BB0, e, la hauteur A0B01−a; l’aire est
donc : A2=(aea+e) ×(1 −a)
2=1 2¡−a2ea+aea−ae+e¢.
b) Aire Ade la partie du plan hachurée :
Si l’on note A3l’aire comprise entre la courbe C, l’axe des abscisses, l’axe des ordonnées et la
droite d’équation x=1, on a : A3=Z1
0xexdx=1 .
Ainsi :
A=A1+A2−A3=a2ea
2+1 2¡−a2ea+aea−ae+e¢−1=1 2¡aea−ae+e−2¢
PARTIE B
Soit gla fonction définie sur [0 ; +∞[ par
g(x)=x¡ex−e¢+e−2.
1. Calcul g0(x) pour tout réel xde [0 ; +∞[ :
g0(x)=(ex−e) +xex
Calcul de la fonction dérivée seconde g00 :
g00(x)=ex+ex+xex=ex(x+2)
2. Variations de la fonction g0sur [0 ; +∞[ :
lim
x→+∞g0(x)=+∞ et g0(0) =1−e<0
g00(x), dérivée de g0, est du signe de x+2>0 sur [0 ; +∞[.
x
g00(x)
g0(x)
0+∞
+
1−e1−e
+∞+∞
e
0
3. Solution de l’équation g0(x)=0 dans l’intervalle [0 ; +∞[. :
La fonction g0est une fonction continue et strictement croissante sur [0 ; +∞[. Elle réalise donc une
bijection de [0 ; +∞[ sur [1 −e; +∞[30. 0 possède un unique antécédent α.
Valeur approchée de αà 10−1près :
(g0(0,5) '−0,2452 <0
g0(0,6) '0,1971 >0=⇒0,5 <α<0,6