Fonctions polynômes du second degré

✐
✐
“MS2_2F5_chapitrecomplet” — 2014/4/12 — 7:00 — page 1 — #1
✐
✐
✐
✐
✐
✐
FONCTIONS
1
Fonctions
polynômes
du second degré
Connaissances du collège nécessaires à ce chapitre
◮Développer une expression littérale
◮Reconnaître un axe de symétrie
◮Additionner des fractions
◮Multiplier des fractions
Auto-évaluation Des ressources numériques pour préparer
le chapitre sur manuel.sesamath.net @
1Développer et réduire les expressions suivantes.
1) (x+1)25) 5(x−1)(x−4)
2) (x−3)26) −2(x−4)(x+2)
3) (x−1, 5)2−2, 5 7) 7(x+7)(x+3)
4) x−1
3!2
−2
38) −1 2 x−1 4!x−2 5
2Calculer les expressions suivantes.
1) 2
3−7 33) −7 6−−4 18
2) 3
14 [phone] −5 8
3Calculer les expressions suivantes.
1) 2
3×3 73) −51 6×12 34
2) 3
−14 ×−21 −64) 12 48 ×5 8
4Déterminer les axes de symétries des figures.
F1F2
F4
F3
➤➤➤Voir solutions p. 17
1

✐
✐
“MS2_2F5_chapitrecomplet” — 2014/4/12 — 7:00 — page 2 — #2
✐
✐
✐
✐
✐
✐
Activités d’approche
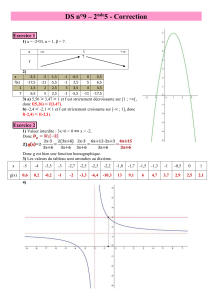
ACTIVITÉ 1Paraboliquement vôtre
On a représenté ci-dessus six fonctions trinômes au 2edegré définies sur R.
Partie 1 : Associations
+
1
+
0.5
0
C1
+
1
+
0.5
0
C2
+
1
+
1
0
C3
+
1
+
1
0
C4+
1
+
1
0
C5+
1
+
1
0C6
1) Associer chacune des fonctions définies sur Rpar les formules ci-dessous à l’une des courbes
représentatives ci-dessus.
•f(x) = 3(x−3)(x−1)•n(x) = −1
2x+1 22
+2
•g(x) = x2•p(x) = 3x2−12x+9
•h(x) = (x+2)2+1•r(x) = −1
5x2−x−13 4
•k(x) = −1
2x−3 2x+5 2•s(x) = 3(x−2)2−3
•l(x) = −x2•t(x) = x2+4x+5
•m(x) = −1
5x+5 22
−2•u(x) = −1
2x2−1 2x+15 8
2) Certaines de ces fonctions ont la même courbe représentative.
a) Regrouper dans un tableau les associations faites à la question 1en les triant par courbe.
b) Quel est le nombre maximum de fonctions associées à une courbe ?
Partie 2 : Images et antécédents
En utilisant l’expression la plus adaptée parmi celles de la question 2a, déterminer,
1) par les fonctions f,g,h,k,let m:
a) les images de 0 ; b) les éventuels antécédents de 0.
2) par les fonctions fpuis k:
a) l’image de 2 ; b) les éventuels antécédents de 1.
Vérifier les calculs par lecture graphique.
Partie 3 : Sens de variation et extremum
1) Établir les tableaux de variations des fonctions représentées par les courbes C3et C6.
2) Comparer ces tableaux et les formes des fonctions représentées.
3) Démontrer ces sens de variations.
2Chapitre F1. Fonctions polynômes du second degré

✐
✐
“MS2_2F5_chapitrecomplet” — 2014/4/12 — 7:00 — page 3 — #3
✐
✐
✐
✐
✐
✐
Cours - Méthodes
1. Forme canonique
DÉFINITION : Fonction polynôme de degré 2
Soit a,b,ctrois nombres réels avec a6=0.
On appelle fonction polynôme de degré 2 toute fonction Pdéfinie sur Rpouvant
être exprimée sous la forme :
P(x) = ax2+bx +c.
On parle aussi de fonction trinôme.
PROPRIÉTÉ
Soit Pune fonction polynôme du second degré exprimée sous la forme P(x) = ax2+bx +c.
Il existe deux nombres réels αet βpermettant d’écrire Psous le forme :
P(x) = a(x−α)2+β.
Cette forme s’appelle forme canonique.
PREUVE Elle est disponible en complément sur le manuel numérique.
2. Étude d’une fonction trinôme
PROPRIÉTÉ : Sens de variations
Soit a,α,βtrois nombres réels et fune fonction polynôme de degré 2 définie sur Rpar sa
forme canonique f(x) = a(x−α)2+β.
Le sens de variation d’une fonction dépend du signe de a.
x
f
avec
a>0
−∞α+∞
ββ
x
f
avec
a<0
−∞α+∞
ββ
PREUVE La preuve est disponible en complément sur le manuel numérique.
PROPRIÉTÉ : Extremum
Soit a,α,βtrois nombres réels.
fune fonction polynôme de degré 2 définie sur Rpar sa forme canonique
f(x) = a(x−α)2+β.
Sur R, la fonction fadmet βcomme extremum. Il est atteint pour x=α.
C’est un maximum si αest négatif.
C’est un minimum si αest positif.
PREUVE Les tableaux de variations établis précédemment prouvent la propriété.
Chapitre F1. Fonctions polynômes du second degré 3

✐
✐
“MS2_2F5_chapitrecomplet” — 2014/4/12 — 7:00 — page 4 — #4
✐
✐
✐
✐
✐
✐
Cours - Méthodes
PROPRIÉTÉ : Signes
Soit a,α,βtrois nombres réels et fune fonction polynôme de degré 2 définie sur Rpar sa
forme canonique f(x) = a(x−α)2+β.
Le signe d’une fonction trinôme dépend du signe de aet du signe de β.
Si a<0 et β60, alors la fonction est toujours négative.
Si a>0 et β>0 alors la fonction est toujours positive.
Dans les autres cas,
la fonction change de signe sur l’intervalle ]−∞;α[;
la fonction change à nouveau de signe sur l’intervalle ]α;+∞[.
PREUVE Les tableaux de variations établis précédemment prouvent la propriété.
MÉTHODE 1 Étudier une fonction trinôme du second degré Ex. 12 p. 6
Exercice d’application On considère la fonction fdéfinie sur Rpar f(x) = −2(x−0, 25)2−8.
Déterminer :
1) son sens de variation ;
2) son extremum;
3) le signe de la fonction.
Correction Dans le cas de la fonction f:
•α=0, 25 •β=−8•a=−2
1) aest négatif donc la fonction fest croissante sur ]−∞; 0, 25[et décroissante sinon.
2) Elle admet un maximum en x=α=0, 25. Il vaut f(0, 25) = −8.
x
f(x)
−∞0,25 +∞
−8−8
3) La fonction fest négative sur R.
3. Représentation graphique
DÉFINITION
La courbe représentative d’une fonction trinôme est une parabole.
PROPRIÉTÉ
Soit a,α,βtrois nombres réels et fune fonction trinôme définie sur Rpar sa forme canonique
f(x) = a(x−α)2+β. La courbe représentative de cette fonction est une parabole qui admet
un axe de symétrie : la droite d’équation x=α.
PREUVE La preuve est disponible en complément sur le manuel numérique.
4Chapitre F1. Fonctions polynômes du second degré

✐
✐
“MS2_2F5_chapitrecomplet” — 2014/4/12 — 7:00 — page 5 — #5
✐
✐
✐
✐
✐
✐
Cours - Méthodes
Exemple Tracer les courbes représentatives des fonctions suivantes :
•f(x) = −0, 5(x+2)2+3
•g(x) = 2(x−3)2−2
Donner leurs sens de variations et leur éventuel extremum.
Correction
+
1
+
1
0
Cg
Cf
La fonction f:
•est croissante sur ]−∞;−2[;
•est décroissante sur ]−2; +∞[;
•elle admet un maximum en −2 qui vaut 3.
La fonction g:
•est décroissante sur ]−∞; 3[;
•est croissante sur ]3; +∞[;
•elle admet un minimum en 3 qui vaut −2.
MÉTHODE 2 Identifier la forme d’une fonction Ex. 25 p. 7
Exercice d’application Soit f,g,htrois fonctions définies sur Rpar :
•f(x) = 2x2+4x−6•g(x) = 2(x+1)2−8•h(x) = 2(x−1)(x+3).
1) Montrer que f,g,hsont trois formes de la même fonction.
2) Répondre aux questions suivantes en utilisant la forme la plus adaptée.
a) Chercher les éventuels antécédents de 0 et de −6.
b) Déterminer les coordonnées du sommet de la courbe représentative de cette fonction.
c) Calculer les images de 0, de 1 et de −1.
Correction
1) On développe get hpour prouver qu’elles sont égales à f.
g(x) = 2(x+1)2−8=2x2+4x+2−8=2x2+4x−6
h(x) = (2x−2)(x+3) = 2x2+6x−2x−6=2x2+4x−6.
fest la forme développée,gla forme canonique et hla forme factorisée du même trinôme.
2) a) Chercher les antécédents, c’est résoudre une équation.
•Pour l’antécédent de 0, la forme la plus adaptée est la forme factorisée.
On résout h(x) = 2(x−1)(x+3) = 0. Les antécédents de 0 sont 1 et −3.
•Pour l’antécédent de −6, la plus pertinente est la forme développée.
On résout f(x) = 2x2+4x−6=−6. On obtient 2x2+4x=0.
On factorise l’expression : x(2x+4) = 0. Les antécédents de −6 sont 0 et −2.
b) Pour chercher les coordonnées du sommet d’une parabole, la forme canonique est la plus
pertinente. Ici, c’est gavec α=−1.
Donc les coordonnées du sommet de la parabole sont (−1; −8).
c) Calculer une image, c’est évaluer une expression. La forme la plus adaptée dépend de x.
•f(0) = −6, l’image de 0 est −6.
•h(1) = 0, l’image de 1 est 0.
•g(−1) = −8, l’image de −1 est −8.
Chapitre F1. Fonctions polynômes du second degré 5