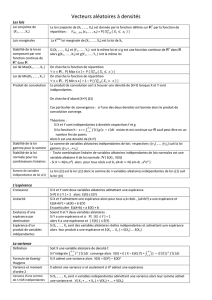
Variables aléatoires réelles discrètes

(Ω,A)
(Ω,A)X: Ω −→ R
∀x∈R, X−1(] − ∞, x]) ∈ A
{ω∈Ω/ X(ω)6x} A
A=P(Ω) Ω R
X X(Ω) X
X X(Ω) X
X(Ω) X X
X(Ω,A)J
R{ω∈Ω/ X(ω)∈J}[X∈J]
J={a}[X=a] = {ω∈Ω/ X(ω) = a}
J=] − ∞, a] [X6a]
J= [a, b[ [a6X < b]

XΩR(Ω,A)
IRX−1(I)A
X k [X=k]A
•[X6x]Ax
•[X < x] =
+∞
k=1
X6x−1
k[X < x]A
A
•[X>x] = [X < x]A
•[X > x] = [X6x]A
•I⊂R[X∈I] = X−1(I)
A
Ω
A=P(Ω)
ω∈ΩX(Ω)
X(ω) = 4 ω
X(ω) = 3 ω
X(ω) = 2 ω
X(ω) = 1 ω
X(ω) = 0
X(Ω) 0,1,2,3,4X(Ω) = {0,1,2,3,4}
Ω = J1,6K×J1,6K={(x, y), x, y ∈J1,6K}
X
X(Ω) = {2,3,...,12}X
p
X X = 0
(Ω,A)Pn
n
k∈N[X=k]A
∀k>1,[X=k] =
k−1
j=1
Pj∩Pk∈ A [X= 0] =
+∞
j=1
Pj∈ A
X X(Ω) = NX
ΩX(Ω)
X X(Ω) = {xi, i ∈I}
([X=xi])i∈I

(Ω,A,P)
X
•X(Ω) = {xi, i ∈I}X
•i∈I pi=P([X=xi])
P([X=xi]) = P(X=xi)
X X(Ω)
xiX(Ω) P(X=xi)
X(Ω)
xiP(X=xi)
X
X(Ω) = {0,1,2,3,4}
[X= 0]
16
P(X= 0) = 16
32 =1 2
[X= 1] P(X= 1) = 4
32 =1 8
P(X= 2) = P(X= 3) = P(X= 4) = 1
8
X
xi01234
pi
1
2
1
8
1
8
1
8
1
8
X X(Ω) = {xi, i ∈I}
i∈I
P(X=xi) = 1
([X=xi])i∈I
A∈ A P(A) =
i∈I
P([X=xi]∩A) =
i∈I
P(X=xi)P[X=xi](A)
{(xi, pi), i ∈I}R2I=N,Z
• ∀i∈I, pi>0
•
i∈I
pi= 1
(Ω,A,P)XΩ{(xi, pi), i ∈I}
X

XFX:R−→ R
∀x∈R, FX(x) = P(X6x)
FXX
•x∈]− ∞,0[ [X6x]FX(x)=0
•x∈[0,1[ X6x X = 0 FX(x) = P(X= 0) = p0=1
2
•x∈[1,2[ FX(x) = p0+p1=5
8
•x∈[2,3[ FX(x) = p0+p1+p2=3
4
•x∈[3,4[ FX(x) = p0+p1+p2+p3=7
8
•x∈[4,+∞[FX(x) = p0+p1+p2+p3= 1
X(Ω,A,P)FX
∀x∈R, FX(x)∈[0,1]
FXR
∀a, b ∈R P(a < X 6b) = FX(b)−FX(a)
lim
x→−∞ FX(x)=0
lim
x→+∞FX(x)=1
FXR
x∈RFX(x) = P(X6x)∈[0,1]
a, b ∈Ra6b[X6a]⊂[X6b]P(X6a)6P(X6b)
FX(x)6FX(y)
a, b ∈R[a<X6b]=[X6b]\[X6a]P(a<X6b) = P(X6b)−P(X6a) =
FX(b)−FX(a)
X(Ω,A,P)FXX(Ω) =
{xi, i ∈I}xii∈I1−i∈I
xi−1< xi
P(X=xi) = FX(xi)−FX(xi−1)

4 1 4
X1X2Y
Y
Y1,2,3,4Y(Ω) = {1,2,3,4}
P(Y6k)P(Y=k)
[Y= 3] = ([X1= 1] ∩[X2= 3]) ∪([X1= 2] ∩[X2= 3]) ∪([X1= 3] ∩[X2= 3]) ∪
([X1= 3] ∩[X2= 1]) ∪([X1= 3] ∩[X2= 2])
[Y63] = [X163] ∩[X263]
FYY FY(1) FY(2) FY(3) FY(4)
FY(1) = P(Y61) = P(Y= 1) = P([X1= 1] ∩[X2= 1]) = P(X1= 1)P(X2= 1) = 1
4×1 4=1 16
FY(2) = P(Y62) = P([X162] ∩[X262]) = P(X161)P(X261) = 2
4×2 4=1 4
FY(3) = P(Y63) = P([X163] ∩[X263]) = P(X163)P(X263) = 3
4×3 4=9 16
FY(4) = P(Y64) = 1
Y
P(Y= 1) = FY(1) = 1
16
P(Y= 2) = FY(2) −FY(1) = 3
16
P(Y= 3) = FY(3) −FY(2) = 5
16
P(Y= 4) = FY(4) −FY(3) = 7
16
X X
X X(Ω) P(X=k)k∈X(Ω)
FXX