Sommaire de la séquence 10

Sommaire de la séquence 10
Séance 1 ........................................................................................................
J’étudie un problème concret . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Séance 2 .......................................................................................................
Je maîtrise le vocabulaire ...................................................................................
Séance 3 .......................................................................................................
J’effectue quelques exercices ..............................................................................
Séance 4 .......................................................................................................
J’étudie un deuxième problème ...........................................................................
Séance 5 .......................................................................................................
Je découvre les polygones réguliers ......................................................................
Séance 6 .......................................................................................................
J’étudie les polygones réguliers ...........................................................................
Séance 7 ........................................................................................................
Je construis des polygones réguliers .....................................................................
Séance 8........................................................................................................
J’étudie les polygones réguliers -suite- ..................................................................
Séance 9 .......................................................................................................
J’effectue des exercices de synthèse ....................................................................
Ce cours est la propriété du Cned. Les images et textes intégrés à ce cours sont la propriété de leurs auteurs et/ou ayants droit
respectifs. Tous ces éléments font l’objet d’une protection par les dispositions du code français de la propriété intellectuelle ainsi que
par les conventions internationales en vigueur. Ces contenus ne peuvent être utilisés qu’à des fins strictement personnelles. Toute
reproduction, utilisation collective à quelque titre que ce soit, tout usage commercial, ou toute mise à disposition de tiers d’un cours
ou d’une œuvre intégrée à ceux-ci sont strictement interdits.
©Cned-2009
Objectifs
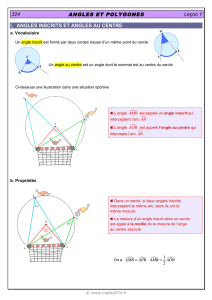
Connaître les notions « d’angle au centre » et « d’angle inscrit » dans un cercle.
Savoir mener des calculs d’angles et de longueurs dans des polygones réguliers.
Être capable d’utiliser un maximum de moyens (tableur, géométrie dynamique, ... ) pour chercher à
résoudre des problèmes.
© Cned – Académie en ligne© Cned – Académie en ligne

Cned, Mathématiques 3e –
213
Séquence 10
Séance 1
J’étudie un problème concret
Avant de commencer cette séance, lis attentivement les objectifs de la séquence n°10.
Effectue ensuite le test ci-dessous directement sur ton livret en cochant la ou les bonnes réponses.
Une fois ce travail terminé, reporte-toi au livret de corrigés et étudie bien le corrigé de ce test. Lis
attentivement les commentaires du professeur : c’est nécessaire pour pouvoir effectuer les exercices
qui suivent dans de bonnes conditions.
JE RÉVISE LES ACQUIS DE LA 4e
1-
O est un point de [AB].
Le segment [AB] est :
 le diamètre du cercle.
 une corde du cercle.
 un rayon du cercle.
 un diamètre du cercle.
2-
A et B sont deux points
d’un cercle de centre O.
La notation
AB
représente :
 l’arc rouge.
 l’arc vert.
 la longueur AB
 le segment d’extrémités A et B.
3- La figure ci-dessous est représentée à main
levée. A et B sont deux points
d’un cercle C de centre O.
Quelle est la mesure de
l’angle
AOB
?
 50°
 70°
 110°
 130°
4- Parmi les figures ci-dessous, lesquelles sont des
polygones ?
 un parallélogramme.
 un cercle.
 un triangle.
 un trapèze.
Prends une nouvelle page de ton cahier de cours et de ton cahier d’exercices puis écris :
« SÉQUENCE 10 : POLYGONES RÉGULIERS ». Effectue l’exercice suivant dans ton cahier
d’exercices. Une fois l’exercice terminé, n’oublie pas de te reporter à son corrigé et de lire
attentivement les deux parties : « Ce que tu devais faire » et « les commentaires du professeur ».
© Cned – Académie en ligne

– Cned, Mathématiques 3e
214
Séquence 10
EXERCICE 1
Un footballeur est placé sur la partie de cercle ci-contre.
Il est représenté par le point M.
Le footballeur essaie de marquer un but.
Problème :
En quel point de ce cercle l’angle de tir
AMB
est-il le plus grand ?
1- Essaie de résoudre le problème pendant 10 minutes.
Aides :
● N’hésite pas à faire des tests à l’aide de la figure ci-contre, ou à utiliser
une figure dynamique, ou autre …
● Si tu veux construire une figure dynamique, lis l’aide de Nadia :
J’ai tracé un cercle de centre O et de rayon 5 cm, puis j’ai placé deux points A et B
sur ce cercle.
J’ai ensuite placé le point M sur le cercle puis j’ai mesuré l’angle
AMB
.
Si tu n’arrives pas à construire la figure dynamique, ouvre le fichier sequence10exercice1question1
à l’aide de Geogebra (c’est la figure toute faite !).
2-
La conjecture qu’il fallait établir lors de la question précédente est : « l’angle de tir est toujours le
même ».
Compare cet angle
AMB
et l’angle
AOB
.
Aides :
● Pour cela, mesure par exemple ci-contre l’angle
AOB
.
● Tu peux aussi utiliser la géométrie dynamique.
Si tu n’arrives pas à construire la figure dynamique, ouvre le fichier
sequence10exercice1question2 à l’aide de Geogebra.
© Cned – Académie en ligne

Cned, Mathématiques 3e –
215
Séquence 10
3-
La conjecture qu’il fallait établir lors de la question précédente est : « l’angle de tir est toujours le
même : c’est la moitié de l’angle
AOB
, où O est le centre du cercle».
Andry, Clément et Pauline vont essayer de démontrer cette conjecture.
a)
Andry essaie de prouver cette conjecture, c’est-à-dire :
2=
AOB AMB
quand les points M, A et O sont alignés.
Il pose : x =
AMB
Il réussit à démontrer que :
2
=
AOB x
après avoir :
● trouvé la nature du triangle OBM,
● calculé la mesure de
BOM
en fonction de x.
Essaie de retrouver la démonstration d’Andry.
b)
Clément essaie de prouver cette conjecture, c’est-à-dire :
2=
AOB AMB
dans le cas ci-contre.
Clément veut utiliser le résultat d’Andry.
Pour cela, il introduit N le 2ème point d’intersection du cercle et de la droite (MO).
● Exprime
AON
en fonction de
AMN
.
● Exprime
NOB
en fonction de
NMB
.
● Déduis de tes deux dernières réponses que :
AOB 2AMB
=.
© Cned – Académie en ligne

– Cned, Mathématiques 3e
216
Séquence 10
c)
Pauline essaie de prouver la conjecture dans le cas ci-contre.
Pauline veut utiliser le résultat d’Andry.
Pour cela, elle introduit N le 2ème point d’intersection du cercle et de la droite (MO).
● Exprime
NOB
en fonction de
NMB
.
● Exprime
NOA
en fonction de
NMA
.
● Déduis de tes deux dernières réponses que :
AOB 2AMB
=.
Pour terminer cette séance, reporte-toi à la fiche de calcul mental n°5. Effectue ensuite la
série 3 de cette fiche.
© Cned – Académie en ligne