Chap 10 – Convexité - Mathématiques 2015-2016

Chap 10 – Convexité
I. Convexité d'une fonction......................................................................................................................4
1) Introduction........................................................................................................................................4
2) Définitions : Fonction convexe, fonction concave.............................................................................4
3) Convexité des fonctions usuelles.......................................................................................................4
4) Lien entre convexité de f et sens de variation de f'.............................................................................5
5) Point d'inflexion.................................................................................................................................5
II. Positions relatives de courbes.............................................................................................................7
A. Gniady – 2015-2016 Chap 10 – Convexité 1 / 7
Chap 10 – Convexité
Terminale ES

A. Gniady – 2015-2016 Chap 10 – Convexité 2 / 7

Vérifier les acquis p 112
Activités : 1 et 2 p 113 (Transmath Activité 1 page 124)
TES.41 Chap 10 – Convexité Exercices
TES.410 Reconnaître graphiquement des fonctions convexes,
concaves.
3 p 115 ; oral : 30, 31 p 122
Feuille n°60 et 61
TES.411 Etudier la convexité à l'aide des variations de la dérivée. 39 à 41 p 25 ; 9 à 13 p 117, 19 p 119 ; 42 à 59 p 123-124
Feuille n°5, 6, 9, 69, 70, 84, 39, 12
TES.412 Reconnaître un point d’inflexion. Feuille n°67, 71
TES.413
Connaître les positions relatives des courbes représentant
les fonctions exponentielle, logarithme népérien et
identité.
4, 5, 6 p 115
TES.414 Comparer deux fonctions. 17 p 119, 38 p 123, 41 p 123 ; 61 à 68 p 125
AP p 120 et 121
Exercices bilan :
76 et 78 p 129, 80 à 83 p 130, 92 p 132
Feuille : 85, 130, 70, 89, 90, 138, 142
TP :
73 p 128 geogebra
A. Gniady – 2015-2016 Chap 10 – Convexité 3 / 7

I. Convexité d'une fonction
1) Introduction
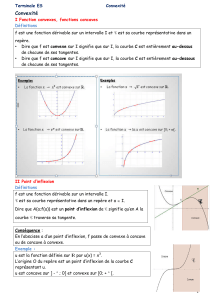
2) Définitions : Fonction convexe, fonction concave
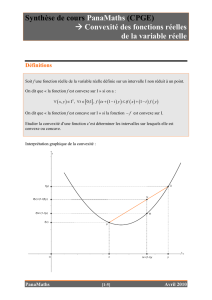
Soit
f
une fonction dérivable sur un intervalle
I
et
Cf
sa courbe représentative dans un repère.
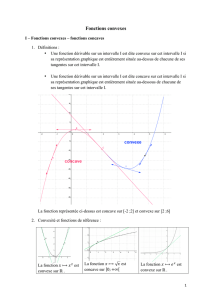
La fonction
f
est dite convexe sur l'intervalle I si sa courbe
Cf
est entièrement située au-dessus de
chacune de ses tangentes.
La fonction
f
est dite concave sur l'intervalle I si sa courbe
Cf
est entièrement située en-dessous
de chacune de ses tangentes.
3) Convexité des fonctions usuelles
•La fonction carré
x→x2
est convexe sur
ℝ
.
•La fonction inverse
x→1
x
est concave sur
ℝ*-
et convexe sur
ℝ*+
.
•La fonction cube
x→x3
est concave sur
ℝ-
et convexe sur
ℝ+
.
•La fonction racine carrée
x→
√
x
est concave sur
ℝ+
.
•La fonction exponentielle
x→ex
est convexe sur
ℝ
.
A. Gniady – 2015-2016 Chap 10 – Convexité 4 / 7
Concave Convexe

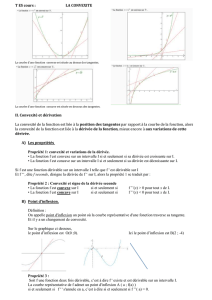
4) Lien entre convexité de f et sens de variation de f'.
Théorème admis :
Soit
f
une fonction dérivable sur un intervalle
I
.
La fonction
f
est convexe si, et seulement si, sa fonction dérivée
f '
est croissante sur l'intervalle
I
.
La fonction
f
est concave si, et seulement si, sa fonction dérivée
f '
est décroissante sur l'intervalle
I
.
Utilisation de la dérivée seconde
Définition : Soit
f
une fonction dérivable sur un intervalle
I
.
On dit que la fonction
f
est deux fois dérivable sur
I
lorsque la fonction dérivée
f '
est elle-même
dérivable sur
I
.
Vocabulaire : Dans ce cas, la dérivée de la fonction
f '
est appelée dérivée seconde de
f
.
On la note
f ' '
.
Propriété : Soit
f
une fonction deux fois dérivable sur un intervalle I.
La fonction
f
est convexe si, et seulement si, pour tout réel
x∈I
,
f ''(x)≥0
.
La fonction
f
est concave si, et seulement si, pour tout réel
x∈I
,
f ''(x)≤0
.
5) Point d'inflexion
Définition :
Un point d'inflexion d'une courbe est un point en lequel la courbe traverse la tangente.
Si une courbe
C
admet un point d'inflexion au point A d'abscisse
a
, alors la fonction
f
change de convexité
en
a
(elle passe de convexe à concave ou inversement).
Propriété admise :
Soit
f
une fonction deux fois dérivables sur un intervalle I et
Cf
sa courbe représentative dans un repère.
Soit
a
un réel appartenant à l'intervalle ouvert I.
Le point A d'abscisse
a
est un point d'inflexion de la courbe
Cf
si, et seulement si, la dérivée seconde
f ' '
s'annule en
a
en changeant de signe.
A. Gniady – 2015-2016 Chap 10 – Convexité 5 / 7