fiche de révision du bac

Annales, corrigés et résultats du BAC à retrouver sur Studyrama.com © Studyrama – Tous droits réservés
FICHE DE RÉVISION DU BAC
LE COURS
[Série – Matière – (Option)]
[Titre de la fiche]
MATHÉMATIQUES – SÉRIES ES / L
LA CONVEXITÉ
Prérequis
Fonctions usuelles – dérivation – fonctions exponentielle et logarithme népérien – tangentes à la courbe
Plan du cours
1. Notions de convexité et de concavité
2. Dérivées premières, dérivées secondes
3. Point d’inflexion
1. Notions de convexité et de concavité
Définitions :
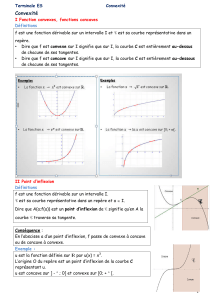
Une fonction est convexe si sa courbe représentative est située au-dessus de ses tangentes.
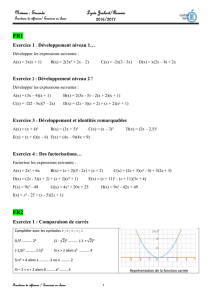
Une fonction est concave si sa courbe représentative est située en-dessous de ses tangentes.
Exemples :
La fonction exponentielle est convexe :
La fonction logarithme est concave :

Annales, corrigés et résultats du BAC à retrouver sur Studyrama.com © Studyrama – Tous droits réservés
FICHE DE RÉVISION DU BAC
LE COURS
[Série – Matière – (Option)]
[Titre de la fiche]
MATHÉMATIQUES – SÉRIES ES / L
LA CONVEXITÉ
D’où l’inégalité suivante, valable pour tout a et pour tout x appartenant au domaine de définition de la fonction :
si f est convexe
si f est concave
Propriété dite « de l’inégalité des milieux » :
- Soit f convexe sur I et a et b deux réels appartenant à I. Alors
- Soit f concave sur I et a et b deux réels appartenant à I. Alors
Remarques :
- Une fonction peut être convexe sur un intervalle, et concave sur un autre. Ex : la fonction cube.
- On peut deviner la convexité d’une fonction à l’allure de sa courbe : si la courbe « sourit », elle est convexe, si elle
« boude », elle est concave.
- Attention : il n’y a pas de lien a priori entre convexité et sens de variation. Une fonction peut être convexe et
croissante, convexe et décroissante, concave et croissante puis décroissante, etc.
- Fonctions usuelles : les fonctions carrée et exponentielle sont convexes. Les fonctions racine carrée et logarithme
népérien sont concaves. La fonction inverse est concave sur et convexe sur . Les fonctions affines
sont à la fois convexes et concaves.
Propriétés :
Produit d’une fonction u par un réel k :
u convexe
u concave
k>0
ku convexe
ku concave
k<0
ku concave
ku convexe
Somme de deux fonctions u et v :
v convexe
v concave
u convexe
u + v convexe
On ne peut pas
conclure
u concave
On ne peut pas
conclure
u + v concave

Annales, corrigés et résultats du BAC à retrouver sur Studyrama.com © Studyrama – Tous droits réservés
FICHE DE RÉVISION DU BAC
LE COURS
[Série – Matière – (Option)]
[Titre de la fiche]
MATHÉMATIQUES – SÉRIES ES / L
LA CONVEXITÉ
2. Dérivées premières, dérivées secondes
Propriétés :
Soit f une fonction dérivable sur un intervalle I.
Si f’ est croissante sur I alors f est convexe sur I. Si f’ est décroissante sur I alors f est concave sur I.
Définition :
La dérivée seconde d’une fonction est la dérivée de sa dérivée. Elle se note f’’.
Ex :
Rappel : si la dérivée est positive alors la fonction est croissante, si la dérivée est négative, alors la fonction est
décroissante. D’où :
Propriétés :
Soit f une fonction dérivable sur un intervalle I.
Si f’’ est positive sur I alors f est convexe sur I. Si f’’ est négative sur I alors f est concave sur I.
Récapitulatif :
f
convexe
concave
f’
croissante
décroissante
f’’
positive
négative
3. Point d’inflexion
Définition :
Un point d’inflexion est un point où la courbe change de convexité.
Elle passe de concave à convexe ou de convexe à concave.

Annales, corrigés et résultats du BAC à retrouver sur Studyrama.com © Studyrama – Tous droits réservés
FICHE DE RÉVISION DU BAC
LE COURS
[Série – Matière – (Option)]
[Titre de la fiche]
MATHÉMATIQUES – SÉRIES ES / L
LA CONVEXITÉ
Propriétés :
- Soit f une fonction définie sur I et a un réel appartenant à I. Si f’’(a) = 0 alors le point d’abscisse a est un point
d’inflexion.
- La tangente au point d’inflexion traverse la courbe.
Exemple :
La fonction cube a pour point d’inflexion O (0 ; 0). La tangente en ce point (d’équation y = 0) traverse la courbe.

Annales, corrigés et résultats du BAC à retrouver sur Studyrama.com © Studyrama – Tous droits réservés
FICHE DE RÉVISION DU BAC
LE COURS
[Série – Matière – (Option)]
[Titre de la fiche]
MATHÉMATIQUES – SÉRIES ES / L
LA CONVEXITÉ