Cours TES convexite

Terminale ES
Convexité
1

TES Convexité
Convexité
f est une fonction dérivable sur un intervalle I et Cest sa courbe
représentative dans un repère.
•Dire que f est convexe sur I signifie que sur I, la courbe Cest
entièrement au-dessus de chacune de ses tangentes.
•Dire que f est concave sur I signifie que sur I, la courbe Cest
entièrement au-dessous de chacune de ses tangentes.
Définitions
2
I Fonction convexes, fonctions concaves

TES Convexité
Convexité
3
Exemples
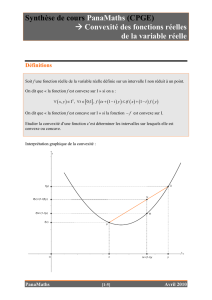
•La fonction  →   est concave sur .
•La fonction  → ln  est concave sur ]0; + ∞[.
Exemples
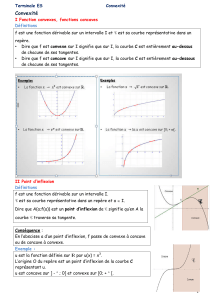
•La fonction  → ² est convexe sur .
•La fonction  → est convexe sur .

TES Convexité
Convexité
f est une fonction dérivable sur un intervalle I.
Cest sa courbe représentative dans un repère
et a ∈I.
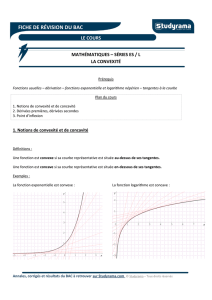
Dire que A(a;f(a)) est un point d’inflexion de C
signifie qu’en A la courbe Ctraverse sa
tangente.
Définition
4
II Point d’inflexion
Conséquence :
En l’abscisse a d’un point d’inflexion, f passe de convexe à concave ou de concave à
convexe.
C

TES Convexité
Convexité
5
Exemple :
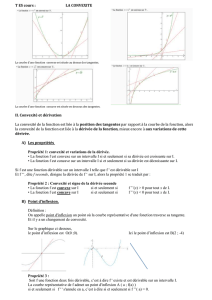
u est la fonction définie sur par u(x) = x3.
L’origine O du repère est un point d’inflexion de la courbe Creprésentant u.
u est concave sur ] - ∞; 0] et convexe sur [0; + ∞[.
C