DS convexité TES 13-14

Devoir surveillé de mathématiques n°8 28/03/14 Term ES
Nom :
Exercice 1(4) : lecture graphique
42 p 123
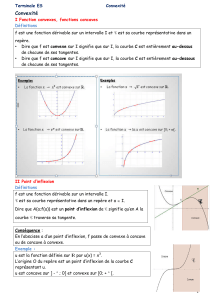
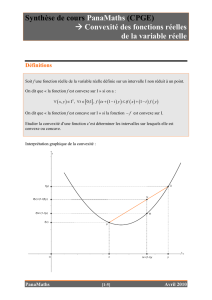
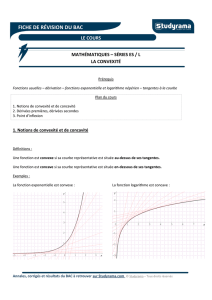
Courbe 1 Courbe 2 Courbe 3
1°) La courbe 1 ci-dessus est celle représentative d'une fonction f sur [-3;3].
Déterminer, par simple lecture graphique, la convexité de cette fonction f.
2°) On considère une fonction g dérivable sur [-4;2], dont la dérivée
g
'
a
pour représentation graphique la courbe 2 ci-dessus.
Déterminer, par simple lecture graphique, la convexité de cette fonction g.
3°) On considère une fonction h deux fois dérivable sur [-4;2], dont la dérivée
seconde
h
'
'
a pour représentation graphique la courbe 3 ci-dessus.
Déterminer, par simple lecture graphique, la convexité de cette fonction h.
Exercice 2 : ( 4,5 )
On considère la fonction f définie sur ℝ par
f
(
x
)=
2
x
3
+
3
x
2
12
x
+
4
.
1°) Étudier la convexité de la fonction f.
2°) Déterminer l'équation de la tangente à
C
f
en son point d'inflexion.
3°) En utilisant les deux questions précédentes, compléter directement sur cet
énoncé par l'intervalle et l'expression algébrique qui conviennent :
∀ x ∈ ….......................,
2
x
3
+
3
x
2
12
x
+
4
>...........................
∀ x ∈ …........................,
2
x
3
+
3
x
2
12
x
+
4
< ….......................
Exercice 3 : (3,5)
On considère la fonction définie sur ℝ
+∗
par f(x)=
ln
(
x
)
3
x
.
1°) Démontrer que f '(x)=
4
ln
(
x
)
x
2
.
2°) a- Résoudre l'inéquation
4
ln
(
x
)>
0
.
(Donner les solutions sous forme d'un intervalle).
b- Effectuer le tableau de variations complet de f sur ℝ
+∗
.
Exercice 4 : ( 8 )
Lors de la propagation d'une rumeur, le nombre d'individus propageant cette
rumeur x jours après son commencement est donné, en unité, par la fonction
f(x)=100+x
4
e
0,1 x
avec x ∈ [0;50]
1°) Déterminer le nombre d'individus propageant cette rumeur initialement.
2°) a- Prouver que
f '(x)= x
2
e
0,1 x
(0,1 x
2
+4x)
.
b- Effectuer le tableau de variation de la fonction f sur [
0
;
50
].
3°) Dans cette question, on admet que la dérivée seconde de
f
est :
f ' '(x)=e
0,1x
×x
2
×(0,01 x
2
0,8 x+12)
Étudier la convexité de la fonction f sur [
0
;
50
].
4°) En déduire :
a- Le nombre de jours qu'il faut attendre avant que le nombre d'individus
propageant cette rumeur diminue (arrondi à l'unité)
b- Le nombre maximum d'individus propageant cette rumeur (arrondi à
l'unité)
c- Le nombre de jours qu'il faut attendre avant que la croissance du
nombre d'individus propageant cette rumeur diminue.

Devoir surveillé de mathématiques n°8 28/03/14 Term ES
Exercice 1(4) :
1°)
Sur [-3;-1,5] et [1,5;3] , les tangentes sont aux dessus de la courbe donc la
fonction est concave.
Sur [
1,5
;
1,5
] , les tangentes sont en dessous de la courbe donc la fonction
est convexe.
2°)
La fonction g est convexe lorsque
g
'
est croissante et concave lorsque
g
'
est décroissante donc : g est convexe sur [
4
;
1
] et [
1
;
2
] et g est
concave sur [
1
;
1
].
3°)
La fonction h est convexe lorsque
h
'
'
est positive, et concave lorsque
h
'
'
est négative.
Donc h est convexe sur [
2
;
1
] et concave sur [
4
;
2
] et [
1
;
2
].
Exercice 2 : (4,5) f(x)=2x
3
+3x
2
12 x+4
1°) Pour étudier la convexité de la fonction f, on va étudier le signe de
f
'
'
:
f '(x)=6x
2
+6x12
f
'
'
(
x
)=
12
x
+
6
f
'
'
est du premier degré et s'annule en 0,5.
x
–∞0,5 +∞
f
'
'
(
x
)+ 0 –
On en déduit que
f
est convexe sur ]∞
;
0,5
] et concave sur [
0,5
;
+∞[
Elle admet un point d'inflexion en 0,5
2°)
Le point d'inflexion est en
0,5
.
L'équation de la tangente en
0,5
est
y
=
f
'
(
0,5
)(
x
0,5
)+
f
(
0,5
)
f
'
(
0,5
)=
10,5
f
(
0,5
)=
1,5
y
=
f
'
(
0,5
)(
x
0,5
)+
f
(
0,5
) ⇔
y
=
10,5
(
x
0,5
)+(
1,5
)
⇔
y
=
10,5
x
+
5,25
1,5
⇔
y
=
10,5
x
+
3,75
3°) Sur ]∞
;
0,5
] la fonction est convexe donc au dessus de ses tangentes
d'où :
∀ x ∈ ]∞
;
0,5
] ,
2
x
3
+
3
x
2
12
x
+
4
> 
10,5
x
+
3,75
Sur ]∞
;
0,5
] la fonction est concave donc au dessous de ses tangentes
d'où :
∀ x ∈
[
0,5
;
+∞[
,
2
x
3
+
3
x
2
12
x
+
4
< 
10,5
x
+
3,75
Exercice 3 : (3,5)
1°) f(x)=
ln
(
x
)
3
x
f =
u
v donc f '=
u
'
v
v
'
u
v
2
avec
u
(
x
)=
ln
(
x
)
3
soit u'(x)=
1
x
v
(
x
)=
x
soit
v
'
(
x
)=
1
f '(x)=
1
x×x1(ln(x)3)
x
2
=1ln(x)+3
x
2
=4ln(x)
x
2
2°) le dénominateur est strictement positif sur ℝ
+∗
4
ln
(
x
)>
0
⇔ 
ln
(
x
)>
4
⇔
ln
(
x
)<
4
⇔
x
<
e
4
On en déduit :
x0
e
4
+∞
4–ln(x) + 0 –
x
2
+ +
f
'
(
x
)
+ 0 –
f(x)
1
e
4

Exercice 4: (8)
1°)
f
(
0
)=
100
donc il y avait 100 personnes au courant de cette rumeur au
départ.
2°) a-
f
=
w
+
uv
donc
f
'
=
w
'
+
u
'
v
+
v
'
u
avec
w
(
x
)=
100
donc
w
'
(
x
)=
0
u
(
x
)=
x
4
donc
u
'
(
x
)=
4
x
3
v
(
x
)=
e
0,1 x
donc
w
'
(
x
)=
0,1
e
0,1x
f '(x)=0+4x
3
×e
0,1 x
+x
4
×(0,1)e
0,1x
f '(x)=e
0,1 x
(4x
3
0,1 x
4
)
f ' ( x )= e
0,1 x
× x
2
( 4x 0,1 x
2
)
f '(x)= x
2
×e
0,1x
×(0,1 x
2
+4x)
b- Effectuer le tableau de variation de la fonction f sur [
0
;
50
].
x
2
est positif sur ]0;50], nul en 0
 ∀ x ∈ ℝ ,
e
0,1 x
>
0
0,1
x
2
+
4
est un trinôme.
=
4
2
4
×(
0,1
)×
0
=
16
Donc deux racines :
x
1
=4
√
16
2×(0,1)=40 et
x
2
=…=
0
On a le tableau de signe de
f
'
et celui de variations de f suivant :
x0 40 50
x
2
0+ +
e
0,1 x
+ +
–
0,1
x
2
+
4
x
0+ 0 –
f
'
(
x
)
0 + 0 -
f(x) 100
100
+
2560000
e
100
+
6250000
e
3°)
0,01
x
2
0,8
x
+
12
est un trinôme qui
=...=0,16
x
1
=...=20 et
x
2
= .... = 60
On en déduit sur [0;50] le tableau de signes de
f
'
'
suivant :
x0 20 50
0,01
x
2
–
0,8
x
+
12
+ 0 –
e
0,1 x
+ +
x
2
0+ +
f
'
'
(
x
)0 + 0 –
La fonction est convexe sur [
0
;
20
] et concave sur [20;50]
4°) En déduire :
a- il faut attendre 40 jours avant que le nombre de personnes propageant
cette rumeur commence à diminuer.
b- Au maximum, il y a
100
+
2560000
×
e
4
≈ 46 988 personnes
c- Le nombre de jours qu'il faut attendre avant que la croissance du
nombre d'individus propageant cette rumeur diminue correspond au
changement de convexité lorsque la fonction est croissante.
En effet, une fonction croissante passant de convexe à concave implique
une diminution de la croissance (une croissance moins forte).
Il faut donc attendre 20 jours avant que la croissance diminue.