THEOREME DE THALES I) Agrandissement et réduction

THEOREME DE THALES
En classe de 4e, on a étudié de nombreuses propriétés de géométrie dont le théorème de Thalès dans
le triangle. Cette année, nous allons étudier sa généralisation et voir sa réciproque qui permet d’avoir
une nouvelle méthode pour montrer que deux droites sont parallèles.
I) Agrandissement et réduction
Activité : une propriété des longueurs d’un triangle
Propriété : Proportionnalité des longueurs dans un triangle
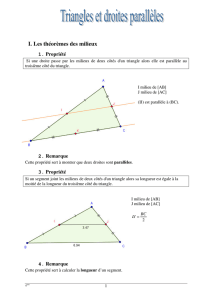
Dans un triangle ABC, soit M un point situé sur le côté [AB], et N un point situé sur le côté [AC].
Si la droite (MN) est parallèle à la droite (BC), alors les longueurs des côtés du triangle AMN sont
proportionnelles aux longueurs des côtés du triangle AMN, et on a le tableau de proportionnalité
suivant :
Côtés du triangle ABC
AB
AC
BC
Côtés du triangle AMN
AM
AN
MN
Sur la figure : les points A, B et M sont alignés
Les points A, C et N sont alignés
Les droites (BC) et (MN) sont parallèles
Le triangle ABC est un agrandissement du triangle AMN.
Toutes les longueurs sont multipliées par le rapport d’agrandissement k, avec k>1.
Le triangle AMN est une réduction du triangle ABC.
Toutes les longueurs sont multipliées par le rapport de réduction k’, avec 0<k’<1.
Les mesures des angles de la figure sont inchangées.

II) Pour calculer une longueur
Activité : propriété de Thalès (elle sert aussi pour montrer la conséquence)
Théorème de Thalès :
(d) et (d’) sont deux droites sécantes en un point A.
B et M sont deux points de (d), distincts de A.
C et N sont deux points de (d’), distincts de A.
Si les droites (BC) et (MN) sont parallèles, alors 
Il y a deux configurations possibles :
1er triangle: A M N
2e triangle: A B C ----- 
III) Pour montrer que deux droites ne sont pas parallèles.
Conséquence du théorème de Thalès :
Lorsque les droites (BM) et (CN) sont sécantes en A :
Si 
  alors les droites (BC) et (MN) ne sont pas parallèles.

IV) Pour montrer que deux droites sont parallèles
Activité : Réciproque de Thalès
Vocabulaire :
Sur chacune des figures, on dit que « les points A, B, M de la droite (d) et les points A, C, N de la
droite (d’) sont dans le même ordre ».
Réciproque du théorème de Thalès :
(d) et (d’) sont deux droites sécantes en A.
B et M sont deux points de (d’), distincts de A.
C et N sont deux points de (d), distincts de A.
Si 
 et si les points A, B, M et les points A, C, N sont dans le même ordre, alors les droites (BC)
et (MN) sont parallèles.