Fonctions polynômes du second degré. Fonctions homographiques

Chapitre 10 : Fonctions polynˆomes du second
degr´e. Fonctions homographiques
I Fonctions trinˆomes du second degr´e
D´efinition
Une fonction du second degr´e est une fonction fqui a expression de la forme f(x) =
ax2+bx +c, o`u a,b,c, sont des r´eels, a6= 0.
Une telle fonction est d´efinie sur R.
D´efinition (et th´eor`eme)
Pour toute fonction polynˆome du second degr´e f(x) = ax2+bx +c, il existe des r´eels α
et βuniques tels que, pour tout x∈R,f(x) = a(x−α)2+β.
L’´ecriture f(x) = a(x−α)2+βest appel´ee la forme canonique de f.
Exercice 1
1. V´erifier que −3(x+ 1)2−4 = −3x2−6x−7.
2. Montrer que 2(x−7)2−1 = 2x2−28x+ 97.
Exercice 2
Mettre sous forme canonique a(x−α)2+β:
1. f(x) = 2x2+ 8x+ 1.
2. g(x) = −3x2+ 12x+ 5
Th´eor`eme (Tableau de variation)
Soit f(x) = a(x−α)2+βune fonction du trinˆome du second degr´e .
Si a > 0,
x−∞ α+∞
f(x)
β
Si a < 0,
x−∞ α+∞
f(x)
β
Exemple :
La fonction carr´e.
1

2
4
6
8
1 2 3-1-2-3-4
Propri´et´e (Courbe repr´esentative)
Soit f(x) = a(x−α)2+βavec a6= 0.
Dans un rep`ere orthogonal, la courbe repr´esentative de fest une parabole :
– tourn´ee vers le haut si a > 0,
– tourn´ee vers le bas si a < 0.
Son sommet est le point S(α;β).
La droite parall`ele `a l’axe des ordonn´ees et passant par le sommet est axe de sym´etrie de
la parabole.
Remarque
En premi`ere, on verra que si f(x) = ax2+bx +c, avec a6= 0, l’abscisses du sommet est
xS=α=−b
2a.
On peut alors d´eterminer le sommet sans passer par la forme canonique :
1. son abscisse est xS=−b
2a,
2. son ordonn´ee est yS=f−b
2a.
Exercice 3
Soit f(x) = x2−6x+ 13.
D´eterminer les coordonn´ees du sommet de la courbe de f.
Pr´eciser comment est tourn´ee la parabole.
Exercice 4
Soit fla fonction du second degr´e dont la courbe passe par A(1; 2) et a pour sommet
B(2; 5).
1. D´eterminer l’expression de f.
2. Dresser le tableau de variation de f.
Exercice 5
1. D´eterminer les coordonn´ees du sommet d’une parabole repr´esentant une fonction
trinˆome du second degr´e de forme canonique donn´ee : ressource 3135
2

2. Dresser le tableau de variations d’une fonction trinˆome du second degr´e de forme
canonique donn´ee : ressource 3133
3. Indiquer l’extremum d’une fonction trinˆome du second degr´e de forme canonique
donn´ee, sa nature et le nombre pour lequel il est atteint : ressource 3138
4. D´eterminer l’axe de sym´etrie de la courbe repr´esentative d’une fonction trinˆome du
second degr´e de forme canonique donn´ee : ressource 3132
5. D´eterminer le nombre d’ant´ec´edents d’un nombre par une fonction trinˆome du second
degr´e suivant les valeurs de ce nombre : ressource 2349
II Fonctions homographiques
D´efinition
Une fonction fest homographique si elle a une expression de la forme f(x) = ax +b
cx +d, o`u
a,b,c, et dsont des r´eels tel que c6= 0 et ad −bc 6= 0.
Un telle fonction est d´efinie pour tout xtel que cx +d6= 0.
Exemple :
Soit f(x) = 3x+ 2
x−5.
Rechercher l’ensemble de d´efinition de f.
Valeur interdite : on r´esout x−5 = 0.
Donc x= 5.
Df=R\ {5}=] − ∞; 5[ ∪]5; +∞[.
Remarque
Que se passe-t-il lorsque c= 0 ?
Lorsque ad =bc ?
Exercice 6
Soit fla fonction d´efinie par f(x) = 2x−2
x+ 1 .
1. D´eterminer l’ensemble de d´efinition de f.
2. D´eterminer le point d’intersection de Cfavec l’axe des ordonn´ees.
3. Rechercher les points d’intersection de Cfavec l’axe des abscisses.
4. Quel est point de Cfqui a pour ordonn´ee 4 ?
5. 2 admet-il des ant´ec´edents par f. Comment cela se traduit-il sur la courbe repr´esentative ?
6. V´erifier que pour tout x6=−1, f(x) = 2 −4
x+ 1.
7. D´eterminer le sens de variation de fsur ] −1; +∞[.
8. En d´eduire un encadrement de f(x) pour x∈[1; 2].
Exercice 7
1. D´eterminer l’ensemble de d´efinition d’une fonction homographique : ressource 2881
2. D´eterminer l’image d’un entier relatif par une fonction homographique : ressource 2025
3. D´eterminer les ant´ec´edents d’un nombre par une fonction homographique : ressource 2064
4. R´esoudre une ´equation de la forme f(x) = ko`u fest une fonction homographique
et kun nombre r´eel : ressource 2835
3

III M´ethode de dichotomie
Il est parfois difficile de trouver les solutions exactes d’une ´equation du type f(x) = 0 sur
un intervalle [a;b].
On cherche alors des solutions approch´ees.
M´ethode par dichotomie :
Soit fune fonction d´efinie sur un intervalle [a;b].
On suppose que l’´equation f(x) = 0 a une unique solution x0dans l’intervalle [a, b].
Pour approcher la solution x0, on r´eduit l’intervalle contenant x0de moiti´e `a chaque ´etape
de l’algorithme. Pour cela on calcule la moyenne mdes deux extr´emit´e de l’intervalle, puis
l’image de mpar f.
On a donc m=a+b
2.
Algorithme de dichotomie
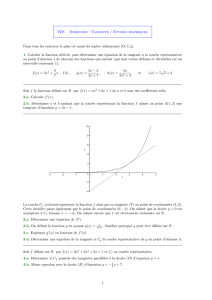
Exemple dans le cas o`u la fonction fest croissante : f(x) = x3−2, sur l’intervalle [1; 2].
1 VARIABLES
2 a EST_DU_TYPE NOMBRE
3 b EST_DU_TYPE NOMBRE
4 m EST_DU_TYPE NOMBRE
5 N EST_DU_TYPE NOMBRE
6 p EST_DU_TYPE NOMBRE
7 DEBUT_ALGORITHME
8 a PREND_LA_VALEUR 1
9 b PREND_LA_VALEUR 2
10 N PREND_LA_VALEUR 0
11 AFFICHER "precision ?"
12 LIRE p
13 TANT_QUE (b-a>p) FAIRE
14 DEBUT_TANT_QUE
15 m PREND_LA_VALEUR (a+b)/2
16 SI (F1(m)>0) ALORS
17 DEBUT_SI
18 b PREND_LA_VALEUR m
19 FIN_SI
20 SINON
21 DEBUT_SINON
22 a PREND_LA_VALEUR m
23 FIN_SINON
24 N PREND_LA_VALEUR N+1
25 FIN_TANT_QUE
26 AFFICHER "Valeur de a : "
27 AFFICHER a
28 AFFICHER "Valeur de b : "
29 AFFICHER b
30 AFFICHER "Nombre d’etapes : "
31 AFFICHER N
32 FIN_ALGORITHME
Fonction numerique utilisee : F1(x)=pow(x,3)-2
4

Exercice 8
1. Recopier cet algorithme dans algobox et l’utiliser pour donner une valeur approch´ee
de la solution de l’´equation x3−2 = 0 par d´efaut `a 10−5 pr`es.
La solution approch´ee `a 10−5par d´efaut est x0≈....
Le nombre d´etape de l’algorithme est : ....
2. On s’int´eresse `a l’´equation 3x5−x3+x2−1 = 0. On pose f(x) = 3x5−x3+x2−1.
(a) Calculer f(0) et f(1).
f(0) = ....
f(1) = ....
(b) On admet que l’´equation a une seule solution x0∈[0; 1], et que fest croissante
sur [0; 1].
Adapter l’algorithme pour donner un encadrement de la solution d’amplitude
inf´erieure `a 10−4. L’encadrement souhait´e est : . . .
Nombre d´etapes : . . .
3. D´esormais f(x) = x4−4x−1 (voir exercice 82 page 67).
L’´equation f(x) = 0 a une unique solution x0dans [−1; 0].
Adapter l’algorithme pour donner un encadrement de la solution d’amplitude inf´erieure
`a 10−4.
Attention : fest d´ecroissante sur [−1; 0].
L’encadrement souhait´e est : . . .
Nombre d’´etapes : . . .
5