Intro: Description cinématique Description cinématique 1. Etude de

TP 11: LES OUTILS DE LA MÉCANIQUE CLASSIQUE
Intro:
Intro: Intro:
Intro: Description cinématique
Description cinématiqueDescription cinématique
Description cinématique
1.
1.1.
1. Etude de mouvements rectilignes
Etude de mouvements rectilignesEtude de mouvements rectilignes
Etude de mouvements rectilignes
Activité distribuée
Activité distribuée Activité distribuée
Activité distribuée -
--
-> enregistrement 1 à faire
> enregistrement 1 à faire> enregistrement 1 à faire
> enregistrement 1 à faire
2.
2.2.
2. Etude de mouvements circulaires
Etude de mouvements circulairesEtude de mouvements circulaires
Etude de mouvements circulaires
Activité p. 89
Activité p. 89Activité p. 89
Activité p. 89

TP 11: LES OUTILS DE LA MÉCANIQUE CLASSIQUE
Intro:
Intro:Intro:
Intro:
a)
a) a)
a) 1:
1: 1:
1: (
((
(traj
trajtraj
traj. =
. = . =
. = ) et
) et) et
) et (v= )
(v= )(v= )
(v= )
2
22
2:
: :
: (
((
(traj
trajtraj
traj. =
. = . =
. = ) et
) et) et
) et (v= )
(v= )(v= )
(v= )
3:
3: 3:
3: (
((
(traj
trajtraj
traj. =
. = . =
. = ) et
) et) et
) et (v= )
(v= )(v= )
(v= )
4
44
4:
: :
: (
((
(traj
trajtraj
traj. =
. = . =
. = ) et
) et) et
) et (v= )
(v= )(v= )
(v= )
b)
b) b)
b) Situation
Situation Situation
Situation Direction
DirectionDirection
Direction Sens
SensSens
Sens Valeur
ValeurValeur
Valeur
1
11
1
2
22
2
3
33
3
4
44
4

TP 11: LES OUTILS DE LA MÉCANIQUE CLASSIQUE
1. Etude de mouvements rectilignes
1. Etude de mouvements rectilignes1. Etude de mouvements rectilignes
1. Etude de mouvements rectilignes
Tracé de vecteurs vitesse et accélération:
Tracé de vecteurs vitesse et accélération: Tracé de vecteurs vitesse et accélération:
Tracé de vecteurs vitesse et accélération:
TP 11: LES OUTILS DE LA MÉCANIQUE CLASSIQUE
2
22
2.
..
. Etude
EtudeEtude
Etude de
dede
de mouvement
mouvementmouvement
mouvement circulaire
circulairecirculaire
circulaire (p
(p(p
(p89
8989
89)
))
)

TP 11: LES OUTILS DE LA MÉCANIQUE CLASSIQUE
2.
2. 2.
2. Mouvement circulaire (p. 89)
Mouvement circulaire (p. 89)Mouvement circulaire (p. 89)
Mouvement circulaire (p. 89)
1.b)
1.b) 1.b)
1.b) v
vv
v2
22
2=
= =
= (1,6
(1,6 (1,6
(1,6 ±
±±
± 0,1) 10
0,1) 100,1) 10
0,1) 10-
--
-1
11
1m.s
m.sm.s
m.s-
--
-1
11
1
3.b)
3.b) 3.b)
3.b) Direction: droite MO et sens: vers O.
Direction: droite MO et sens: vers O.Direction: droite MO et sens: vers O.
Direction: droite MO et sens: vers O.
3c)
3c) 3c)
3c) Le point O.
Le point O.Le point O.
Le point O.
3d)
3d) 3d)
3d) (v
(v(v
(v2
22
2)²/ R = 1,6.
)²/ R = 1,6.)²/ R = 1,6.
)²/ R = 1,6. 10
1010
10-
--
-1
11
1m/ 2,0.10
m/ 2,0.10m/ 2,0.10
m/ 2,0.10-
--
-2
22
2=8,0 m.s
=8,0 m.s=8,0 m.s
=8,0 m.s-
--
-2
2 2
2
et a=
et a= et a=
et a= m.s
m.sm.s
m.s-
--
-2
22
2
Donc
Donc Donc
Donc mvt
mvtmvt
mvt circulaire
circulaire circulaire
circulaire unfiorme
unfiormeunfiorme
unfiorme :
: :
: a=
a=a=
a=
I.
I. I.
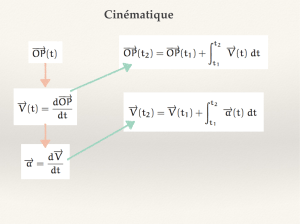
I. CINEMATIQUE
CINEMATIQUECINEMATIQUE
CINEMATIQUE
I.1
I.1I.1
I.1 Référentiel
RéférentielRéférentiel
Référentiel: repère d’espace(x, y, z;
: repère d’espace(x, y, z; : repère d’espace(x, y, z;
: repère d’espace(x, y, z; Frenet
FrenetFrenet
Frenet:
: :
:
mouvements circulaires) et de temps (horloge)
mouvements circulaires) et de temps (horloge)mouvements circulaires) et de temps (horloge)
mouvements circulaires) et de temps (horloge)
=  
  +
Mouvement
Mouvement Mouvement
Mouvement = Trajectoire + vitesse
= Trajectoire + vitesse= Trajectoire + vitesse
= Trajectoire + vitesse

II. DYNAMIQUE
II. DYNAMIQUEII. DYNAMIQUE
II. DYNAMIQUE
Les mouvements sont dus à des
Les mouvements sont dus à des Les mouvements sont dus à des
Les mouvements sont dus à des forces
forcesforces
forces
ETUDE
ETUDE ETUDE
ETUDE DYNAMIQUE EN ETAPES
DYNAMIQUE EN ETAPESDYNAMIQUE EN ETAPES
DYNAMIQUE EN ETAPES :
::
:
1.
1. 1.
1. Définition du système et du référentiel
Définition du système et du référentielDéfinition du système et du référentiel
Définition du système et du référentiel
2.
2. 2.
2. Bilan des forces
Bilan des forcesBilan des forces
Bilan des forces
3.
3. 3.
3. Application de la 2
Application de la 2Application de la 2
Application de la 2ème
èmeème
ème loi de Newton (III.2)
loi de Newton (III.2)loi de Newton (III.2)
loi de Newton (III.2)
Exemple
ExempleExemple
Exemple :
: :
: Luge trainée par une corde le long d’une pente
Luge trainée par une corde le long d’une penteLuge trainée par une corde le long d’une pente
Luge trainée par une corde le long d’une pente
1.
1. 1.
1. Système
SystèmeSystème
Système :
: :
: {Luge} et
{Luge} et {Luge} et
{Luge} et référentiel
référentielréférentiel
référentiel terrestre (surface de la Terre)
terrestre (surface de la Terre)terrestre (surface de la Terre)
terrestre (surface de la Terre)
2.
2. 2.
2. BDF
BDFBDF
BDF :
: :
: Poids
Poids Poids
Poids , Tension du fil
, Tension du fil , Tension du fil
, Tension du fil , Réaction du support
, Réaction du support , Réaction du support
, Réaction du support (la
(la (la
(la
pente).
pente).pente).
pente).
3
33
3. PFD:
. PFD: . PFD:
. PFD: m
m m
m 
= Σ
= Σ = Σ
= Σ 
=
= =
= +
++
+ +
+ +
+ 
Et
Et Et
Et on projette sur les axes x et y pour trouver la valeur de a
on projette sur les axes x et y pour trouver la valeur de aon projette sur les axes x et y pour trouver la valeur de a
on projette sur les axes x et y pour trouver la valeur de a.
..
.On
On On
On
peut ensuite calculer
peut ensuite calculer peut ensuite calculer
peut ensuite calculer v
v v
v et x, y.
et x, y.et x, y.
et x, y.
II. LES TROIS LOIS DE NEWTON
II. LES TROIS LOIS DE NEWTONII. LES TROIS LOIS DE NEWTON
II. LES TROIS LOIS DE NEWTON
1
11
1ère
èreère
ère loi:
loi:loi:
loi: Σ
ΣΣ
Σ=
= =
= =
= =
= 
 ; avec p=
; avec p=; avec p=
; avec p=m.v
m.vm.v
m.v
les forces se compensent.
les forces se compensent.les forces se compensent.
les forces se compensent.
La quantité de mouvement est conservée.
La quantité de mouvement est conservée.La quantité de mouvement est conservée.
La quantité de mouvement est conservée.
Le système est pseudo
Le système est pseudoLe système est pseudo
Le système est pseudo-
--
-isolé (mouvement rectiligne
isolé (mouvement rectiligne isolé (mouvement rectiligne
isolé (mouvement rectiligne
et uniforme ou isolé)
et uniforme ou isolé)et uniforme ou isolé)
et uniforme ou isolé)
2
22
2ème
èmeème
ème loi:
loi:loi:
loi: Σ
ΣΣ
Σ=
= =
= m
m m
m =
= =
= 
3
33
3ème
èmeème
ème loi
loiloi
loi:
::
:/=
= =
= -
--
-/ ;
; ;
; Exemple:
Exemple: Exemple:
Exemple: la Terre et la lune.
la Terre et la lune.la Terre et la lune.
la Terre et la lune.