chap6-lois_newton_exo_1smp

1
1SMP Cours Physique
Chap6 : Les 3 lois de Newton (Ze very retour of…) : exercices
* Exercice 1 Un traîneau …stalgique ! (saouls venirs, souvenirs… de 2S1)
Le traîneau du Père Noël de masse m = 120 kg, tiré par ses rennes, glisse à
vitesse constante, sur un sol horizontal. Les rennes exercent une force de 400 N
sur la corde qui fait un angle = 30° avec l’horizontale. On donne g = 10 N/kg.
1) Il y a-t-il des frottements entre le sol et le traîneau ?
2) Représenter précisément l’action du sol sur le traîneau notée
R
, par
une construction graphique (échelle 1 cm représente 400 N).
3) Déterminer, par le calcul, l’intensité R de l’action du sol sur le traîneau,
ainsi que l’angle que fait cette force avec la verticale.
* Exercice 2 Une dernière descente ?
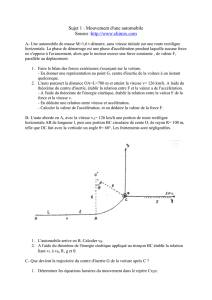
Un enfant prend place sur une luge au sommet O
d’une piste enneigée parfaitement plane, de longueur
l = OB = 50 m et de dénivellation OH = h = 10 m.
L’ensemble forme un solide de masse m = 55 kg.
Les forces de frottements exercées par le sol sur la
luge sont équivalentes à une force unique de valeur
f = 44 N. On négligera les frottements de l’air et on
prendra g = 10 N/kg.
1) A t0 = 0, un autre enfant donne au système une
vitesse initiale en O suivant l’axe (O,x) de
valeur v0x = 2,0 m/s.
a) Déterminer l’expression littérale de la composante ax de l’accélération et calculer sa valeur en donnant 2 chiffres
significatifs.
b) En déduire l’équation horaire du mouvement, c’est-à-dire l’expression de la position x du système (comptée à partir du
point O) en fonction du temps t.
c) Calculer la durée
t de la descente. Ecrire le résultat avec 2 chiffres significatifs.
d) Déterminer la valeur vxB de la vitesse en B en donnant 2 chiffres significatifs.
2) Au bas de la pente, la luge arrive sur une piste horizontale ; les forces de frottements gardent la même valeur. On admet
qu’en B, à la rupture de la pente, il n’y a pas de modification de la valeur de la vitesse.
a) Déterminer l’expression littérale de la composante ax’ de la nouvelle accélération et calculer sa valeur de en donnant 2
chiffres significatifs.
b) En déduire l’équation horaire du mouvement sur cette partie de trajectoire.
c) Calculer la distance parcourue avant l’arrêt. Ecrire le résultat avec 2 chiffres significatifs.
H
h
O
B
x
x’

2
* Exercice 3 prendre la tangente
Cette expression familière signifie partir, se
sauver, s’esquiver…Mais d’où vient-elle ?
L’étude d’un mobile sur une table à coussin d’air
peut en donner une idée.
Le mobile est accroché à un fil inextensible dont
l’autre extrémité est liée à un point fixe O. Le
mobile est lancé à t0 avec une certaine vitesse v0.
A un moment donné, le fil casse.
On étudie le mouvement de son centre d’inertie C
dans le référentiel terrestre.
L’enregistrement de droite est une vue de dessus
à l’échelle réelle. La durée entre deux positions
consécutives est de = 28 ms.
1) Quelle est la nature du mouvement ? (caractériser précisément les différentes phases).
2) A quel instant le fil casse ? Quelle direction prend le mobile au moment de la rupture du fil ?
3) Relire le titre de l’exercice, sourire, puis remercier votre prof pour vous avoir éclairci une expression française…
4) Phase 1 : avant la rupture du fil.
a) Le principe d’inertie est-il respecté ? Vérifiez votre réponse en proposant un bilan des forces effectué sur un schéma
clair.
b) Calculer les valeurs des vitesses instantanées v1 et v3 en m/s.
c) Tracez les vecteurs vitesses
1
v
et
3
v
en choisissant une échelle pratique.
d) Calculer la valeur de l’accélération instantanée a2 en m/s2.
e) Tracez le vecteur accélération
2
a
au point C2 en choisissant une échelle pratique.
f) Que constatez-vous ? Expliquer ce constat.
g) En déduire une estimation de la vitesse instantanée v2.
h) Ecrire la 2ème loi de Newton pour le mobile (PFD) au point C2.
i) En projetant le PFD sur un axe pratique, trouver la valeur de la tension du fil sachant que la masse du mobile est m =
600 g.
5) Phase 2 : après la rupture du fil.
Le principe d’inertie est-il respecté ? Vérifiez votre réponse en proposant un bilan des forces effectué sur un schéma clair.
* Exercice 4 le pendule conique (karagoua)
On considère un pendule formé d’une petite boule A (considérée ponctuelle) de masse
m = 200 g située à l’extrémité d’un fil de longueur l = 50 cm et de masse négligeable.
Le pendule est mis en mouvement de rotation uniforme autour d’une tige verticale à la
vitesse angulaire = 50 tr/min. Le fil s’écarte alors d’un angle par rapport à la tige (voir
figure). On prendra g = 9,81 N/kg.
1) Déterminer l’expression de l’accélération centripète en fonction de
, l et
2) En projetant le PFD sur un axe bien choisi, déterminer en fonction de , l et g
l’expression de l’angle que prend le fil par rapport à la tige. Calculer la valeur de
l’angle en donnant un nombre correct de chiffres significatifs.
3) Montrer qu’un tel mouvement n’est possible que si la vitesse angulaire est supérieure à
une valeur que l’on calculera (en tr/min).
Une animation pour comprendre : http://ressources.univ-lemans.fr/AccesLibre/UM/Pedago/physique/02/meca/pendconi.html