La trigonométrie est la partie des mathématiques qui étudie les

Page 1 sur 3
C HAPITRE 4 T RIGONOMETRIE
La trigonométrie est la partie des mathématiques qui étudie les relations entre
les longueurs et les angles des triangles.
I. V OCABULAIRE
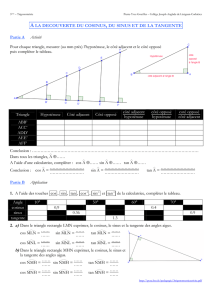
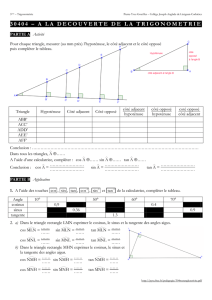
Dans un triangle ABC rectangle en A :
II. D EFINITIONS DANS LES TRIANGLES RECTANGLES
Parler du cosinus, du sinus ou de la tangente d’un angle droit ou d’un angle obtus (plus
grand que l’angle droit) n’a pas de sens au collège.
Pour l’instant on définit seulement le cosinus, le sinus et la tangente d’un angle aigu.
Cosinus d’un angle aigu = longueur du côté adjacent
longueur de l’hypoténuse Cos B = AB BC
Sinus d’un angle aigu = longueur du côté opposé
longueur de l’hypoténuse Sin B = AC BC
Tangente d’un angle aigu = longueur du côté opposé
longueur du côté adjacent Tan B = AC AB
Hypoténuse Côté opposé
à l’angle B
Côté adjacent
à l’angle B

Page 2 sur 3
III. A PPLICATION AUX CALCULS DE LONGUEURS
A. E XEMPLES
 Enoncé 1
Calculer la longueur AC.
Donner l’arrondi au dixième de cm près.
Solution :
Appelons x la mesure en centimètres de la longueur AC.
Dans le triangle ABC rectangle en A : Tan B = AC
AB
Tan (40°) = x
3 Voir paragraphe B pour un aide sur la résolution de cette équation.
x = 3 × Tan(40°)
La valeur exacte de la longueur AC est 3 ×
××
× Tan (40°) cm.
La valeur arrondie au dixième de centimètre est 2,5 cm.
 Enoncé 2
Calculer la longueur ST.
Donner l’arrondi au dixième de cm près.
Solution :
Appelons x la mesure en centimètres de la longueur TS.
Dans le triangle RST rectangle en T : Sin T = RS
TS
Sin (63°) = 6
x Voir paragraphe B pour un aide sur la résolution de cette équation.
x = 6
Sin(63°)
La valeur exacte de la longueur TS est 6
Sin(63°) cm.
La valeur arrondie au dixième de centimètre est 6,7 cm.

Page 3 sur 3
B. A IDE SUR LA RESOLUTION DES EQUATIONS RENCONTREES
Il est possible d’utiliser la règle des produits en croix pour résoudre les équations
rencontrées.
Tan (40°) = x
3 Sin (63°) = 6 x
Tan (40°)
1 = x 3 Sin (63°) 1 = 6 x
x × 1 = 3 × Tan(40°) x × Sin(63°) = 6 × 1
x = 3 × Tan(40°) x × Sin(63°) = 6
x = 6
Sin(63°)
IV. A PPLICATION AUX CALCULS D ’ ANGLES
Enoncé :
Calculer la mesure de l’angleB.
Arrondir au degré près.
Solution :
Dans le triangle ABC rectangle en A :
Cos B = AB
BC
Cos B = 4
6
Donc B = Cos-1
4
6 Note : Garder la valeur exacte 4 6 pour faire le calcul.
La mesure arrondie au degré près de l’angle B est 48°.