Théorème 1

ROTATION, ANGLES ET POLYGONES REGULIERS
I Angle inscrit et angle au centre.
1) Définitions
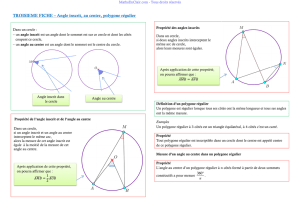
Soit un cercle de centre O et trois points A, B et M appartenant à ce cercle. L'angle
AOB est un angle au centre qui intercepte l'arc de cercle AB (en rouge). L'angle AMB
est un angle inscrit qui intercepte l'arc de cercle AB.
2) Théorème 1
Si un angle inscrit et un angle au centre interceptent le même arc de cercle alors la
mesure de l’angle inscrit est égale à la moitié de la mesure de l’angle au centre.
3) Théorème 2
Si deux angles inscris dans un cercle interceptent le même arc, alors ils ont la même
mesure.
II Rotation
1) Définition
Soit un point O et un angle a.
Par la rotation de sens direct (c'est-à-dire dans le sens des aiguilles d’une montre),
de centre O et d’angle a :
 L’image d’un point A, distinct de O, est le point A’ tel que
OA’ = OA et AOA’ = a.
 L’image de O est O lui-même (O est invariant par la rotation)
2) Propriétés :
 L’image d’une droite par une rotation est une droite.
 L’image d’un segment par une rotation est un segment de même longueur.
 L’image d’un angle par une rotation est un angle de même mesure.
 L’image d’un cercle par une rotation est un cercle de même rayon.

3) Exemple
III Polygones réguliers
Pour information : les noms des principaux polygones se trouvent sur : http://humbert.maths.free.fr/polygones.html
1) Définition
Un polygone régulier est un polygone qui a tous ses côtes de la même longueur et
tous ses angles de même mesure.
2) Exemples
Triangle équilatéral Carré Pentagone régulier Hexagone régulier
Le losange (non carré) ou un triangle isocèle (non équilatéral) ne sont pas des polygones réguliers.
3) Théorème 1
Un polygone régulier est inscriptible dans un cercle. On appelle centre du polygone
régulier, le centre du cercle.
4) Théorème 2
Soient un polygone régulier de centre O et A et B deux sommets consécutifs de ce
polygone.
La rotation de centre O qui transforme A en B transforme le polygone régulier en lui-
même. Le polygone régulier est invariant par cette rotation d’angle 360° : n (nombre
de côtés du polygone)