Notion de bijection, de nouvelles fonctions usuelles

©Arnaud de Saint Julien - MPSI Lycée La Merci 2016-2017 1
Programme de colle n°5 de la semaine n°8 et 9 du 03/11 au 09/11
Notion de bijection. De nouvelles fonctions de référence
Dans tout le chapitre Eet Fdésignent des parties de Ret les fonctions considérées sont réelles. Nous
généraliserons plus tard dans l’année le concept de bijection pour des applications quelconques.
Questions de cours
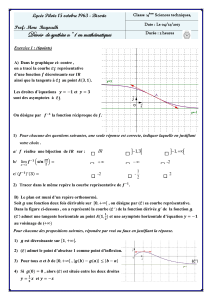
1. f:x7→ x+3
x−2est une bijection de R\ {2}vers R\ {1}et f−1:x7→ 2x+3 x−1.
2. g:x7→ e−x+1
1+x2bijective de R+sur [0,2[, on a g(0) = 2, g′(0) = −1 donc g−1dérivable en 2 et
(g−1)′(2) = 1
g′(0) =−1.
3. Pour x∈[−1,1],sin(arccos x) = cos(arcsin x) = p1−x2.
4. arcsin′(x) = 1
√1−x2P ourx>0,arctan x+ arctan 1
x=π 2
1 Notion de bijection et de fonction réciproque
1.1 Vocabulaire
5. Définition 1 Une fonction f:E→Fest dite bijective si tout élément de Fadmet un unique antécédent
dans Epar f. Cela revient à dire que pour tout y∈F, il existe un unique x∈Etel que f(x) = y. Cet élément
xest noté f−1(y). On définit ainsi l’application réciproque de fnotée f−1de Fdans Equi à un élément y
associe son unique antécédent par f.
On a alors par définition,
∀x∈E, f−1(f(x)) = xet ∀y∈F, f(f−1(y)) = y.
De plus les courbes Γfet Γf−1de fet f−1sont symétriques par rapport à la droite d’équation y=x, car
pour tout x∈Eet y∈F, on a :
(x, y)∈Γf⇐⇒ y=f(x)⇐⇒ x=f−1(y)⇐⇒ (y, x)∈Γf−1.
Exemples modèles :
• la fonction carrée est une bijection de R+sur R+et la fonction racine carrée est sa fonction réciproque.
• la fonction ln :]0 + ∞[→Rest bijective et son application réciproque est exp : R→]0,+∞[.
1.2 Comment prouver qu’une fonction f:E→Fest bijective ?
1. Méthode 1 algébrique : montrer que tout élément yde F, admet un unique antécédent xdans Epar f,
c’est résoudre l’équation f(x) = yd’inconnue x(on doit trouver une unique solution). L’expression de x
en fonction de ydonne alors l’expression de la fonction réciproque.
2. Méthode 2 avec de l’analyse : (corollaire du TVI) : si fest continue et strictement monotone sur un
intervalle I, alors fest une bijection de Isur l’intervalle f(I). Par exemple :
• si f: [a, b]→Rest continue et strictement décroissante, alors fest une bijection de [a, b] sur
[f(b), f(a)]
• si f: [a, b[→Rest continue et strictement croissante, alors fest une bijection de [a, b[ sur [f(a),limbf[.
Attention cette méthode donne l’existence de la fonction réciproque mais ne permet pas d’obtenir son
expression.

©Arnaud de Saint Julien - MPSI Lycée La Merci 2016-2017 2
Exemples :
• (*) f:x7→ x+3
x−2est une bijection de R\ {2}vers R\ {1}et f−1:x7→ 2x+3 x−1.
•g:x7→ e−x+1
1+x2est une bijection de R+dans g(R) = [0,+2[ car fest continue et strictement
décroissante sur R(somme) et a pour limites ...
• Les fonctions racines n-ièmes x7→ n
√x:
Si nest impair, la fonction f:x7→ xnest une bijection de Rsur R. Cela revient à dire que tout réel
xadmet une unique racine n-ième réelle, notée n
√x. Comme on a aussi (x1
n)n=x1 n×n=x1=x, on en
déduit que n
√x=x1
n. La fonction réciproque est donc f−1:x7→ x1 n.
Si nest pair, la fonction x7→ xnest une bijection de R+sur R+, on note x7→ x1/n sa fonction réciproque.
1.3 Qualités conservées par une application réciproque
Le tableau suivant résume les théorèmes ci-dessous : soit f:I→Jbijective.
fcroissante sur I f−1croissante sur J
fest continue sur I f−1est continue sur J
fest dérivable en a∈Iet f′(a)6= 0 f−1est dérivable en b=f(a) et (f−1)′(b) = 1
f′(a)
fest impaire f−1est impaire
On admet pour le moment les théorèmes suivants utiles pour toute la suite du chapitre (nous les démontrerons
plus tard dans l’année) :
Théorème 2 (Théorème de la bijection monotone) Toute fonction fcontinue et strictement monotone
sur un intervalle Iest bijective de Isur l’intervalle J=f(I)et sa fonction réciproque f−1est continue sur J
et possède la même monotonie que f.
Théorème 3 (Théorème de dérivation des fonctions réciproques) Si de plus, fest dérivable en a∈I
avec f′(a)6= 0, alors f−1est dérivable en b=f(a)et on a
(f−1)′(b) = 1
f′(f−1(b)) .
Remarques :
• si fbijective, une tangente horizontale en a(resp. horizontale) pour fdonnera une tangente verticale en
b=f(a) (resp. horizontale) pour f−1par la symétrie par rapport à la droite d’équation y=x.
• pour retrouver la formule précédente, on peut dériver la relation f−1(f(x)) = x, ce qui donne par dérivation
de fonctions composées :
(f−1)′(f(x)) ×f′(x) = 1 donc (f−1)′(f(x)) = 1
f′(x).
Exemples :
• (*) si on reprend g:x7→ e−x+1
1+x2, on a g(0) = 2, g′(0) = −1 donc g−1dérivable en 2 et (g−1)′(2) =
1
g′(0) =−1.
•h:x7→ (x−1)5bijection de Rdans R,h(1) = 0 et h′(1) = 0, donc h−1n’est pas dérivable en 0 et sa
courbe présente une tangente verticale.

©Arnaud de Saint Julien - MPSI Lycée La Merci 2016-2017 3
2 Fonctions circulaires réciproques
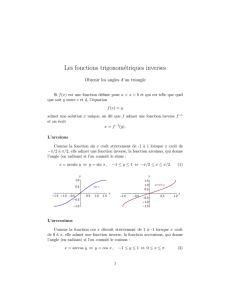
1. Fonctions arcsin et arccos.
À savoir absolument :
• Comment sont-elles définies ? (merci théorème de la bijection). Quelles sont leur variation, leur parité ?
• Savoir calculer cos(arccos x) ou arccos(cos x) selon les valeurs de x(idem avec sin).
• (*) Pour x∈[−1,1],sin(arccos x) = cos(arcsin x) = p1−x2.
• arcsin et arccos sont dérivables sur ]−1,1[ (et non pas sur [−1,1], ce sont des fonctions «méchantes»).
On a
(∗) arcsin′(x) = 1
√1−x2et arccos′(x) = −1 √1−x2.
2. Fonction tangente
On pose pour x6=π
2mod π, tan x=sin x cos x.
tan est π-périodique, impaire, il suffit de l’étudier sur ] −π
2,π 2[. Elle est dérivable (quotient) et
tan′(x) = 1
cos2x= 1 + tan2x.
Elle est donc continue et strictement croissante sur I=] −π
2,π 2[, elle réalise donc une bijection de Isur
tan(I) = R.
On a la formule d’addition
tan(a+b) = tan a+ tan b
1−tan atan b.
3. Fonction arctangente
On note arctan la fonction réciproque de tan restreinte à ]−π
2,π 2[. Elle est définie sur R, impaire car tan|I
l’est, et croissante. Elle est dérivable et arctan′(x) = 1
1 + x2.
On en déduit un nouvel équivalent usuel : arctan x∼0x.
(*) Pour x > 0, arctan x+ arctan 1
x=π 2. (ramène l’étude de arctan à l’infini à son étude en 0).
3 Fonctions hyperboliques
1. Fonctions sinus, cosinus hyperboliques
On pose
∀x∈R,ch x=ex+ e−x
2et sh x=ex−e−x 2.
Les fonctions ch et sh sont dérivables sur Ret on a ch′= sh et sh′= ch . On en déduit leur variation. Il
faut connaître les limites et le graphe.
Remarque : On a les équivalents suivants :
ch x∼+∞
ex
2et sh x∼+∞
ex
2.
On a la relation suivante de trigonométrie hyperbolique :
∀t∈R,ch2t−sh2t= 1 .
Cette relation s’interprète graphiquement : le point de coordonnées (ch t, sh t) est sur l’hyperbole d’équation
x2−y2= 1.

©Arnaud de Saint Julien - MPSI Lycée La Merci 2016-2017 4
2. Fonction tangente hyperbolique. On pose pour x∈R,th(x) = sh x
ch x.
th dérivable et
∀x∈R,th′(x) = 1
ch2x= 1 −th2x.
La fonction th réalise une bijection de Rsur ] −1,1[.
Remarque : les fonctions hyperboliques réciproques ne sont plus au programme. On peut néanmoins les
aborder en exercice.