La fluctuation d`échantillonnage consiste à comparer les fréquences

Module 10 : fluctuation d'échantillonnage
Peut s'étudier à partir d'une expérience aléatoire, pour laquelle il est impossible de prévoir le résultat: celui-ci est soumis
au hasard.
Exemples classiques d'expériences aléatoires:
–lancer une pièce de monnaie et s'intéresser à la face visible;
–lancer un dé et s'intéresser au numéro de la face supérieure;
–tirer une boule dans une urne contenant des boules de diverses couleurs et s'intéresser à la couleur de la boule
obtenue.
La fluctuation d'échantillonnage consiste à comparer les fréquences obtenues (f) en
modifiant le nombre d'essais à la fréquence théorique ( probabilité d'apparition p ).
Exemple : lancer de pièces
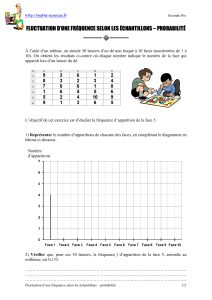
Enoncé: On lance deux pièces et on note le nombre de côtés piles obtenues à chaque lancer.
1)Lister le nombre de cas possibles en réalisant un arbre de probabilité et en déduire la fréquence théorique .
2)Effectuer 50 lancers et lister les résultats obtenus dans un tableau. Comparer avec la fréquence théorique.
3)Regrouper avec les lancers de 9 autres élèves ( 500 lancers au total) . Comparer avec la fréquence théorique.
4)Conclure.
5) Lancers virtuel à la calculatrice:
Il faut d'abord modéliser le problème: pour représenter les résultats d'un lancer, on cherchera à obtenir un nombre égal
soit à 0 (0 pile) , 1 ( 1 pile) ou 2 ( 2 piles) .
On utilisa la fonction "Rand" qui permet de générer un nombre au hasard entre 0 et 1 ( 1 non compris) et la fonction "Int"
qui prend la partie entière du nombre
Relation entre la probabilité d'obtenir un nombre compris entre 0 et 1 et celle d'obtenir le côté « pile »:
soit x le nombre généré par la fonction « rand », alors:
0≤x1
avec
P x∈ [ 0;0,5 [ =P x∈ [ 0,5 ;1 [ =1
2
en multipliant par deux:
0≤2x2
avec
P 2x∈ [ 0;1 [ =P 2x ∈ [ 1;2 [ =1
2
En prenant ensuite la partie entière de 2x:
Ent 2x = { 0;1 }
avec
P 0 =P 1 =1
2
Ces valeurs de probabilités sont donc les mêmes que la probabilité d'obtenir le
côté pile pour un lancement.
Donc, pour obtenir un résultat égal à 0,1 ou 2, la formule nécessaire est:
a) Calculatrice et calcul manuel : : Int(Rand*2)+Int(Rand*2) Touches accessibles par la touche
MATH
b) Calculatrice et programmation : créer un programme permettant de faire l'opération ci-dessus en mettant
commevariable d'entrée le nombre d'entrée.
But: Construire l'algorithme permettant, sachant le nombre de lancers à effectuer, de donner le nombre de 0, de 1 et de 2
obtenus; voir de donner ces résultats sous forme de pourcentage.
- Simuler avec votre machine 50 lancers . Comparer avec la fréquence théorique.
- Augmenter le nombre de lancers . Que constate-t-on ?