Calcul des propositions: syntaxe, sémantique

LOGIQUE 203 A Brève présentation du calcul des propositions 1. Arbres et tableaux sémantiques
Un argument consiste en une suite finie de phrases, les prémisses, et d’une autre, la conclusion que les prémisses étayent
(i) Il pleut ou il neige (ii) Si W est réélu, alors Hillary a une chance en 2008 (iii) Caïn sentait mauvais et Abel sentait bon
Il ne neige pas Hillary a une chance en 2008
______________ ___________________ _______________
Il pleut W sera réélu Caïn sentait mauvais
Un argument est déductivement valide si et seulement si ( « ssi ») sa conclusion est vraie quand ses prémisses sont vraies
Un argument est sain si et seulement si il est valide et ses prémisses sont vraies
Un ensemble de propositions en implique une autre ssi la vérité de celle-ci est garantie par la vérité de celles-là.
Une proposition A est équivalente à une proposition B ssi A et B ont la même valeur de vérité
propositions ( phrases, énoncés)
valide ( tautologie, logiquement vraie) contingente contradictoire
vraie dans toutes les circonstances vraie dans certaines circonstances, fausse dans d’autres fausse dans toutes les circonstances
satisfiable
vraie dans certaines circonstances
Un ensemble de phrases est satisfiable (consistant) ssi elles peuvent être vraies ensemble
Un ensemble de phrases est contradictoire ssi il est impossible que tous ses membres soient vrais
SYNTAXE du calcul des propositions
1. propositions (phrases, énoncés) : p, q, r, s …
2. connecteurs : ne pas () , et (&) , ou () , si…alors () , si et seulement si (  )
3. parenthèses : ( , )
4. Règles de formation :  toute lettre de proposition est une formule
 si est une formule,  A est une formule
 si A et B sont des formules alors A & B, A  B, A B, et A  B sont des formules
5. langage-objet ( p, q, r..) vs metalangage ( A, B, C)
6. propositions atomiques (sans composants) ; propositions complexes ( qui ont des propositions comme composants)
7. portée d’un connecteur : l’occurrence du connecteur avec les composants qu’il lie
8. connecteur principal : celui qui a la portée la plus large
SEMANTIQUE
1. propositions vraies ( V) ou fausses (F)
2. connecteur vérifonctionnel : ssi les valeurs de vérité des propositions composantes déterminent la valeur de vérité des
propositions complexes formées à partir du connecteur
3. fonction de vérité : fonction qui prend n valeurs de vérité comme arguments et produit une valeur de vérité comme valeur.
négation p  p conjonction p q p&q p q disjonction pq p q conditionnel pq p q biconditionnel p  q
V F V V V V V V V V V V V
F V V F V F V V F F V F F
F V F V V F V V F V F
F F F F F F F F F F V
Interpretation d’ une lettre de proposition. Forme d’argument. Validité d’une formule ( vraie sous toutes les interprétations).
Validité d’une forme d’argument (si toute interprétation qui rend les formules prémisses vraies rend aussi la conclusion vraie).
Un ensemble de formules S en implique une autre ssi toute interprétation de S avec A qui rend tout membre de S vrai rend aussi A
vraie. Equivalence de deux formules : si elles s’accordent en valeur de vérité sous toutes les interprétations. Un ensemble de
formules est satisfiable ssi sous une interprétation chaque membre de l’ensemble est vrai. Une formule est une tautologie (vérité
logique) ssi elle est vraie sous toutes les interprétations ; contradictoire si elle est fausses sous toutes ses interprétations.
Une méthode de décision pour une propriété P est une méthode mécanique pour déterminer si un objet a P.
Un ensemble est décidable ssi il y a une procédure de décision pour cet ensemble.
La méthode des tables de vérité est une méthode de décision pour les formules de CP ( satisfiabilité, équivalence, implication
d’ensembles de formules). 2n lignes pour n lettres de propositions. (donc par exemple une formule de 18 lettres requiert 262.144
rangées, et la table aurait 31.000 000 de V et F dans les colonnes).
(i) p  q (ii) p  q (iii) p & q
 p q
______ _______ _____
q p p
Ces inférences sont-elles valides ? Faire une table de vérité. Mais comment éviter de faire une table trop longue ?
Travailler à rebours : supposer que les prémisses sont vraies et la conclusion est fausse.
Une inférence est (vérifonctionnelement) valide ssi il n’y a aucune interprétation qui rende ses prémisses vraies et sa
conclusion fausse ( ou s’il n’y a pas de contre exemple à cette inférence).

Arbres
A B A & B V A & B F A  B  V  (A & B)   ( A & B)
V V V
V F F V A FA F B V  A V  B  A B
F V F
F F F V B A  A  A
 B B  B
A B A  B V A  B F A  B A  B  ( A  B )
V V V
V F V F A  A
F V V V A V B F B A B  B
F F V
A  B  (A  B ) A  B  (A  B )
 A B A A  A A A
 B B B B B
V  A F  A  A   A ( double négation)
F A V A  A A
 Une branche d’un arbre est fermée ssi une formule et sa négation apparaissent dessus
 Un arbre est fermé ssi toute branche est fermée ; autrement il est ouvert
 Un arbre ouvert indique que l’ensemble des formules qui le forment sont satisfiables conjointement
 Un arbre est terminé ssi (i) il est fermé ou (ii) seules des formules atomiques et leurs négations y figurent
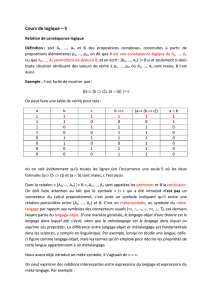
(i) p  q (ii) p  q (iii) p & q
 p q
______ _______ _____
 q  p  p
p q  p q p
X X X
Test pour la validité d’un argument
A1
An
 B
Ferme : valide ; A1 … An impliquent B
Ouvert : non valide ; A1 … An n’ impliquent pas B
Exemples p  q implique-t-il p  q ?
 p &  q implique-t-il  ( p  q) ?
p et p  r implique-t-il r ?
p  q ,  p  q /  q ?
Test pour l’équivalence de A et de B Test pour une tautologie Test pour contradiction
ou satisfiabilité
A B  A A
B  A ferme : A tautologie ferme : contradictoire
ferme : A implique B ferme B implique A ouvert : A contingent ouvert : satisfiable
A et B équivalents ou contradictoire
Exemples (p  ( q  r) )  ( ( p  q)  ( p  r) )